SyntaxNet :Globally Normalized Transition-Based Neural Networks
Daniel Andor, Chris Alberti, David Weiss, Aliaksei Severyn et.al
Google Inc
Abstract
我们设计了一个全局正则化的基于转移的神经网络模型(a globally normalized transition-based neural network),在POS,依赖解析,语句压缩达到了最好的效果。我们的模型是一个在特定trainsition任务上简单的前向传播神经网络,与其它模型相比,准确率更高。我们讨论了global normalization及local normalization:一个重要的概念是标签的偏差意味着globally normalized 模型比locally normalized模型更严格的表达。
Introduction
NN在NLP领域应用广泛,LSTM在POS,语法解析,语义角色标注应用广泛。一个观点是因为循环神经网络才得到这样的效果
我们验证了使用仅globally normalized,精度也能达到甚至超过使用RNN的模型。详见第二节。我们不使用任何循环结构,但用集束搜索验证多个假设,并使用条件随机场(CRF)目标引入globally normalized,以克服locally normalized所遇到的标签偏差问题(???读不懂)。由于我们使用集束推断,我们通过对集束中的元素求和来近似分割函数,并使用早期更新(Collins和Roark,2004; Zhou等,2015)。 我们基于该近似全局归一化来计算梯度,并基于CRF损失对所有神经网络参数执行完全反向传播训练。
章节3重新回顾了下标签偏差问题,说明globally normalized 模型比local normalized模型能更严格的表达。我们的模型在词性标注POS,依赖解析和语句压缩上取得最好的精度,特别是华尔街日报的依赖解析达到历史最好94.61%。
章节5中,我们模型也优于以前用于基于神经网络转换的解析的结构化训练方法。为了在实践过程中进一步阐述标签偏差问题,我们提供了一个语句压缩的例子,其中local 模型几乎完全失败。然后我们证明了没有任何lookahead features的globally normalized模型几乎与我们的最佳模型一样准确。
最后,我们提供了一个名为SyntaxNet的方法的开源实现,我们已将其集成到流行的TensorFlow框架中。 我们还提供了一个预先训练的,最先进的英语依赖解析器,名为“Parsey McParseface”,我们在速度,简单性和准确性方面进行了调整。
2 Model
我们的模型是增量式基于转移的解析器。将它应用到不同的任务上只需要调整transition system和 input feature。
2.1 Transition system
对于输入 $x$,通常是一个语句,我们定义:
- 状态集合$S(x)$
- 特定的开始符号 $S^{\dagger} \in S(x)$
- 允许的决策集合 $A(s,x)$, 所有的$s \in S(x)$
- 转移函数 $t(s,d,x)$, 对任一决策$d \in A(s,x)$返回一个新的状态$s^\prime$
我们会使用函数 $\rho(s,d,x;\theta)$ 来计算输入$x$在状态$s$做决策$d$的得分。向量 $\theta$ 包含模型的所有参数,我们认为 $\rho(s,d,x;\theta)$ 和 $\theta$ 是不同的表示。
本节中,我们省略$x$,函数记为 $S,A(s),t(s,d),\rho(s,d;\theta)$。
在整个工作中,我们使用transition system,相同输入$x$的完整结构,具有相同数量$n(x)$(或简单记为n)的决策。例如,在依赖解析中,arc-standard 和 arc-eager transition system 都是如此,对于长度为$m$的语句输入$x$,完整解析的决策为$n(x) = 2 \times m$。完整结构(complete structure) 是决策/状态序列 $(s_1,d_1)…(s_n,d_n)$, $s_1= s^{\dagger}, d_i \in S(s_i)$, 每个$i = 1…n$, $s_{i+1} = t(s_i,d_i)$。我们用 $d_{1:j}$ 来表示决策序列$d_1…d_j$。
我们认为决策序列 $d_{i:j}$ 和状态 $s_j$是一对一映射:也就是说,我们基本假设一个状态编码了整个决策历史。因此每个序列可以通过从 $S^{\dagger}$ 开始的唯一的决策序列得到。决策序列 $d_{1:j-1}$ 和状态可替换表示,我们定义 $\rho(d_{1:j-1},d;\theta)$ 与 $rho(s,d;\theta)$等同,其中s是 $d_{1:j-1}$ 到达的状态。
得分函数的定义有很多种,我们通过前向传播神经网络来定义:
$$\rho(s,d;\theta)=\phi(s;\theta^{(l)}) \cdot \theta^{(d)}.$$
$\theta^{(l)}$ 是神经网络出去最后一层的所有参数。$\theta^{(d)}$ 是对决策$d$的最后一层参数。 $\phi(s;\theta^{(l)})$ 表示神经网络在参数 $\theta^{(l)}$ 计算得到的状态 $s$。注意,在参数 $\theta^{(d)}$下得分是线性的。我们之后会解释 softmax-style normalization 是如何应用在global和local级的。
2.2 Global vs. Local Normalization
在Chen&Manning(2014)的贪婪式神经网络解析中,在上下文 $d_{1:j-1}$ 下决策 $d_j$ 的条件概率分布定义如下:
$$p(d_j | d_{1:j-1;\theta}) = \frac{\exp \rho(d_{1:j-1}, d_j; \theta)}{Z_L(d_{1:j-1}; \theta)} \tag{1}$$
其中:
$$Z_L(d_{1:j-1}; \theta) = \sum_{d^\prime \in A(d_{1:j-1})} \exp \rho(d_{1:j-1},d^\prime; \theta)$$
每一个 $Z_L(d_{1:j-1}; \theta)$是一个 local normalization 项。决策序列 $d_{1:n}$ 的概率为:
$$
p_L(d^{1:n} = \prod_{j=1}^n p(d_j | d_{1:j-1; \theta})\
=\frac{\exp \sum_{j=1}^n \rho(d_{1:j-1, d_j; \theta})}{\prod_{n=1}^{n}Z_L(d_{1:j-1}; \theta)}. \tag{2}
$$
集束搜索尝试找到Eq.(2)的最大化。集束搜索终得附加分是对每个决策使用logsoftmax,$\ln p(d_j | d_{1:j-1}; \theta)$,而不是原始分数 $\rho(d_{1:j-1}, d_j; \theta)$。
相反,条件随机场(CRF)定义的 $p_G(d_{1:n})$ 如下:
$$
p_G(d_{1:n}) = \frac{\exp \sum_{j=1}^n \rho(d_{1:j-1}, d_j; \theta)}{Z_G(\theta)} \tag{3}
$$
其中,
$$
Z_G(\theta) = \sum_{d_{1:n}^\prime \in D_n} \exp \sum_{j=1}^n \rho(d_{1:j-1}^\prime, d_j^\prime; \theta)
$$
$D_n$是所有的长度为n的有效决策序列集合, $Z_G(\theta)$是global normalization 项。现在推断问题成为找到:
$$\text{argmax}_{d_{1:n} \in D_n} = \text{argmax}_{d_{1:n}\in D_n} \sum_{j=1}^n \rho(d_{1:j-1}, d_j; \theta).
$$
可以再次使用集束搜索来找到近似argmax。
2.3 Training
训练数据是由输入 $x$ 和 gold decision 序列 $d_{1:n}^$ 组合而成。我们使用随机梯度下降和对数似然估计(negative log-likehood)函数。在 locally normalized model中,negative log-likehood 函数为:
$$ L_{local}(d_{1:n}^;\theta) = -\ln p_L(d_{1:n}^;\theta) = \ -\sum_{j=1}^n \rho(d_{1:n}^, d_j^; \theta) + \sum_{j=1}^n\ln Z_L(d_{1:n}^; \theta) \tag{4}$$
而globally normalized model 的似然估计函数为:
$$ L_{global}(d_{1:n}^;\theta) = -\ln p_G(d_{1:n}^;\theta) = \ -\sum_{j=1}^n \rho(d_{1:n}^, d_j^; \theta) + \sum_{j=1}^n\ln Z_G(d_{1:n}^*; \theta) \tag{5}$$
locally normalized 的一个显著优势是公式4中 $Z_L$及其导数计算快速有效。而Eq.5中 $Z_G$ 项在很多情况下是难以处理的。
为了使globally normalized 模型更易学习,我们使用集束搜索和early updates。随着训练序列解码,我们记录集束中的gold path,如果gold path落在 $j$ 布集束之外,将对以下目标进行随机梯度步骤:
$$L_{global-beam}(d_{1:n}^:\theta) = \
-\sum_{i=1}^j \rho(d_{1:i-1}^;\theta) + \ln \sum_{d_{1:j} \in \mit{B_j} } \exp \sum_{i=1}^j \rho(d_{1:n}^\prime, d_i^\prime; \theta) . \tag{6}$$
其中, $\mit{B}j$ 是 $j$ 步集束的所有路径, 前缀 $d{i:j}^*$。可以直接计算Eq.6 中loss的梯度,并反向传播。如果gold path 在整个解码过程中保留,则使用解码结束后的集束 $\mit{b_n}$执行梯度步骤。
3 The Label Bias Problem
直观来讲,我们希望模型能够在发现错误后,能够修改之前的决策错误。乍一看,使用集束搜索或其它确定搜索结合的locally normalized模型能够修改之前的决策。但是label bias问题(see Bottou (1991), Collins (1999) pages 222-226, Lafferty et al. (2001), Bottou and LeCun (2005), Smith and Johnson (2007))说明其在这方面能力非常弱。
本节通过证明全局规范化模型比局部规范化模型更具表现力,证明了标签偏差问题的正式观点。
Global Models can be Strictly More Expressive than Local Models
来考虑将输入序列 $x_{1:n}$ 映射成决策序列 $d_{1:n}$任务中的 tagging problem。首先,考虑到locally normalized 模型, 在对决策 $d_i$ 评分时,我们将限制评分函数取到前 $i$ 个输入符号 $x_{1:i}$。 评分函数 $rho$ 可以是元组 $\langle d_{1:i-1}, d_i, x_{1:i}\rangle$ 的其他任意函数:
$$
p_L(d_{1:n} | x_{1:n}) = \prod_{i=1}^n p_L(d_i|d_{1:i-1}, x_{1:i}) \
= \frac{\exp \sum_{i=1}^n \rho(d_{1:i-1}, d_i, x_{1:i})}{\prod_{i=1}^n Z_L(d_{1:i-1}, x_{1:i})}
$$
其次,考虑 globally normalized模型:
$$p_G(d_{1:n} | x_{1:n}) = \frac{\exp \sum_{i=1}^n \rho(d_{1:i-1}, d_i, x_{1:i}) }{Z_G(x_{1:n})}$$
这个模型同样的得分函数,在对决策 $d_i$ 评分时,限制于前 $i$ 个输入。
定义 $\mit{P_L}$ 为locallly normalized 模型下得分 $\rho$ 所有可能的分布集合 $P_L(d_{1:n} | x_{1:n})$。同理,可以定义 globally normalized 模型$P_G$。这里的“分布”是一个从 $(x_{1:n}, d_{1:n})$ 到概率 $p(d_{1:n}|x_{1:n}$。我们的主要结果如下(证明可参考论文)。
4 Experiments
我们在POS,依赖解析,语句压缩三个任务上进行实验。
4.1 POS
数据集:
- the English Wall Street Journal (WSJ) part of the Penn Treebank
- the English “Treebank Union” multi-domain corpus containing data from the OntoNotes corpus version 5
- the CoNLL ’09 multi-lingual shared task
Model Configuration
Result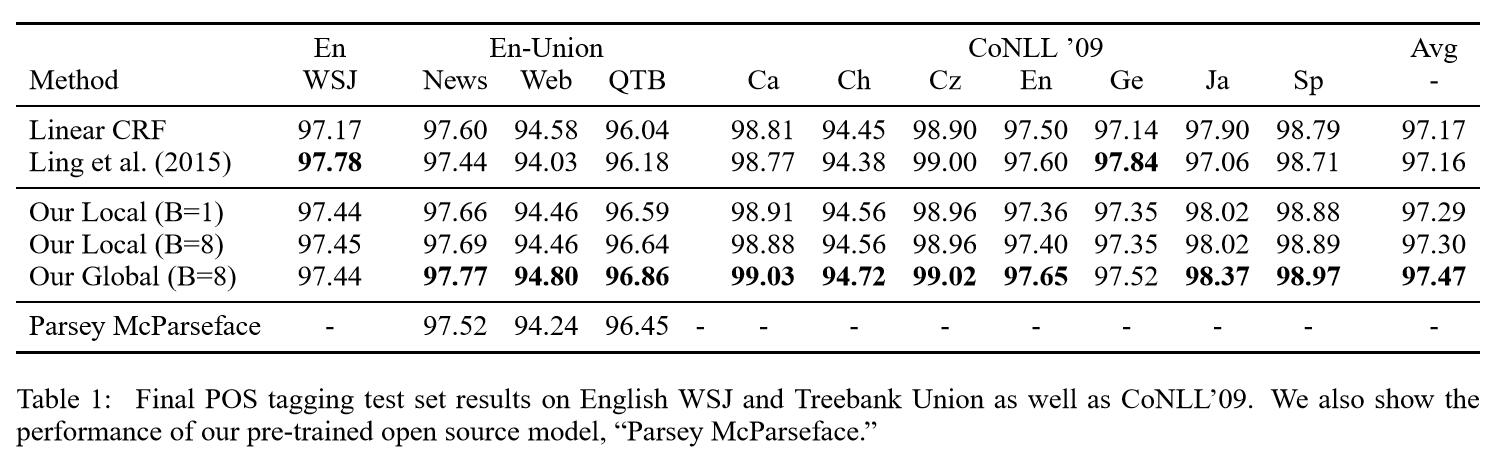
4.2 依赖解析
数据集
与POS任务数据集一样,此外,使用WSJ的标准依赖切分。
Model Configuration
与 Chen and Manning (2014)一致。
Result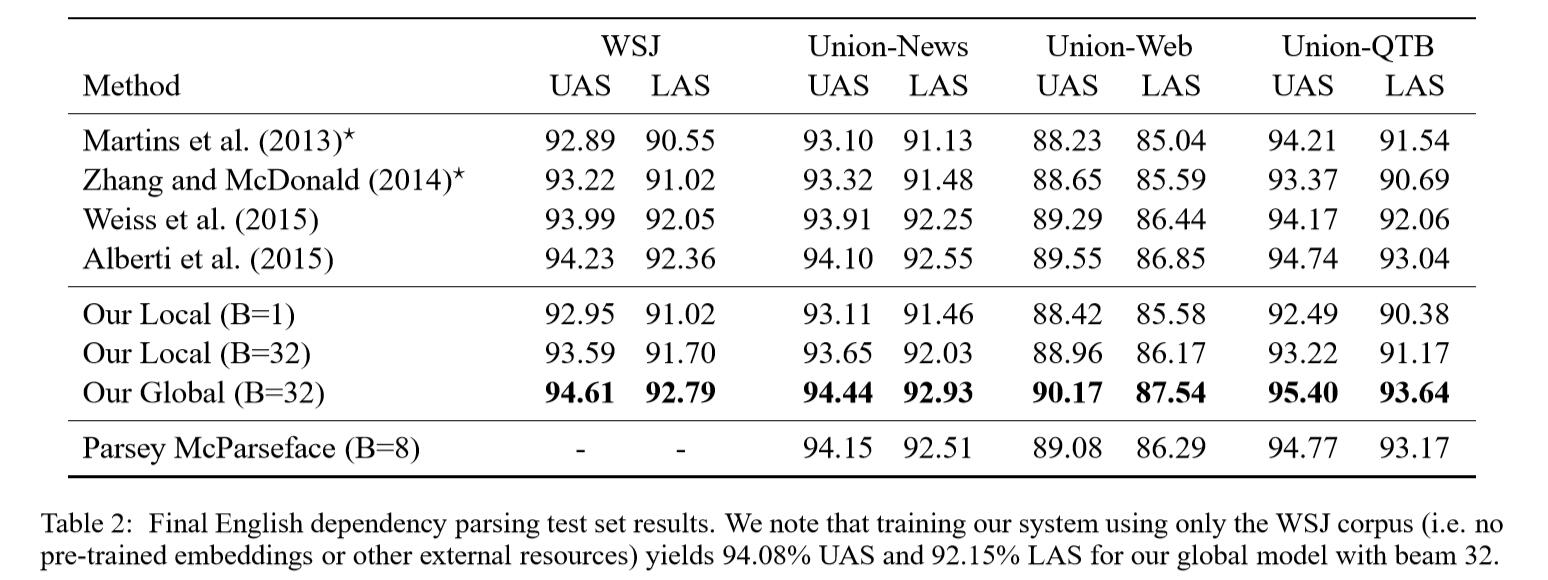
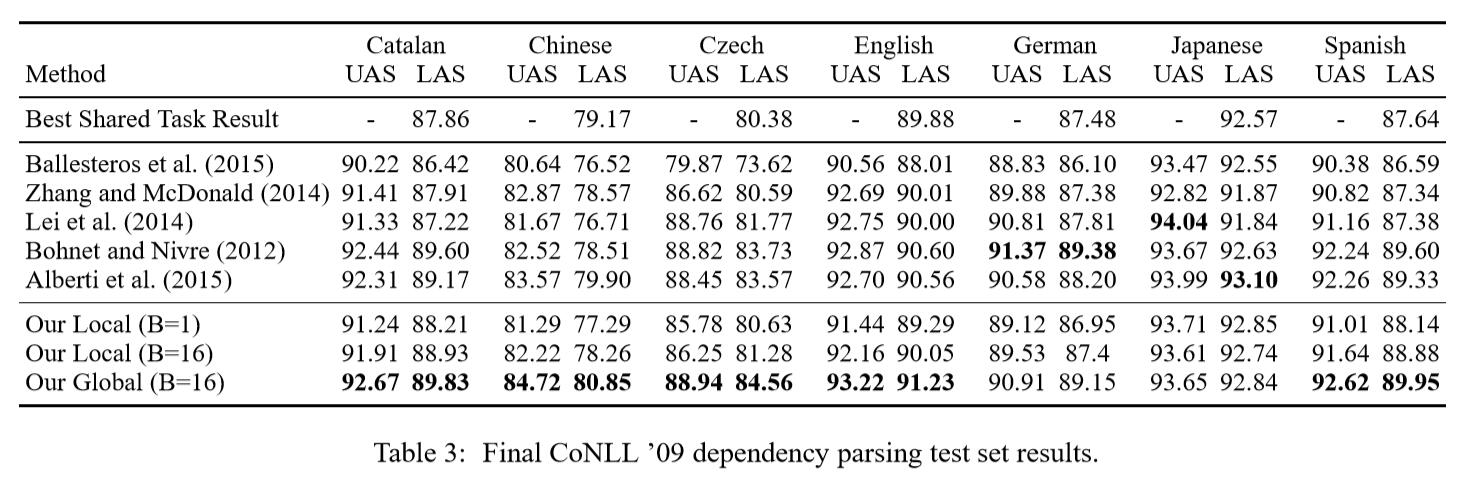
4.3 语句压缩
数据集
Filippova(2015)数据集。
Model Configuration
与transition system相似,将左右替换成keep和drop。
Result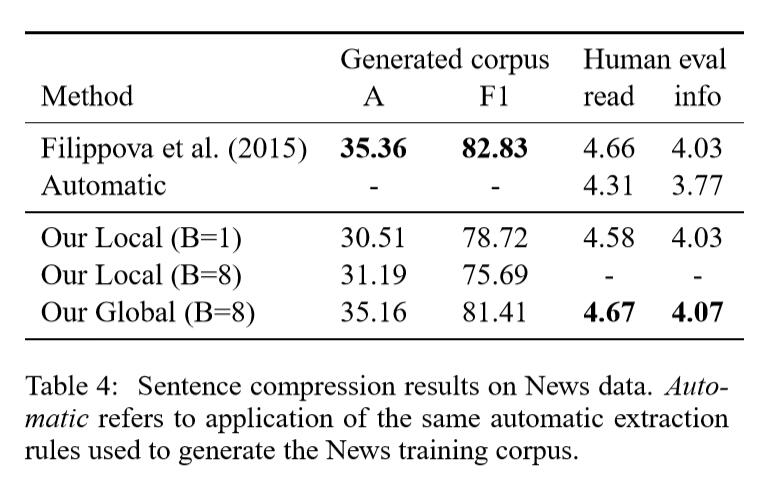
5 Discussion
略
6 Conclusion
我们提出了一种简单但功能强大的模型体系结构,可为POS标记,依赖性解析和句子压缩生成最好的结果。 我们的模型结合了 transition-based 的算法的灵活性和神经网络的建模能力。 我们的研究结果表明,没有循环的前馈网络在通过全局规范化训练时可以胜过LSTM等RNN模型。 我们进一步支持我们的实证结果,证明全局标准化有助于模型克服局部标准化模型所遭受的标签偏差问题。