Attention论文列表
- Sequence to Sequence Learning with Neural Networks, 2014. 机器翻译(Machine Translation)领域论文,使用两个RNN进行机器翻译,亮点在于将source sentence做了逆向输入。未看
- Neural Machine Translation by Jointly Learning to Align and Translation, 2015. 同样属于MT领域,作者认为将source sentence由Encoder映射成一个向量,无法突破翻译瓶颈,并提出了动态搜索relevant part of source sentence, 即Attention思想。未看
- Effective Approaches to Attention-based Neural Machine Translation, 2015. 论文提出了global attention 及 local attention, 博文对其做了比较详细的解释,我也会在下面详细介绍。
- Attention is All You Need, 2017. self-attention机制及Transformer模型。
- Pointer Sentinel Mixture Models, 2016. cs224n课程曾提到过的,当时并没理解。李宏毅老师的课程视频也有讲解。以往的RNN模型虽然对输入序列长度适应,但输出的序列仍然属于固定的集合。Pointer模型能从输入序列中学习输出单词,从而解决模型无法输出未学习到的单词情况。
- Listen, Attend and Spell, 2015. 李宏毅老师曾调侃Attenion模型一定要以三个动词开始。
Attention模型之一详解
参考论文Effective Approaches to Attention-based Neural Machine Translation及完全解析RNN, Seq2Seq, Attention注意力机制(知乎专栏)。
“attention”产生于机器翻译领域,其含义是允许模型学习不同任务间的对齐(learn alignments between different modalities),比如图片描述生成,语音识别。神经机器翻译(NMT)相比于传统MT,占用内存小,decoder实现简单以及end-to-end。
NMT系统是神经网络模型在条件概率$p(y|x)$下将source sentence,$x_1,…,x_n$ 翻译成target sentence, $y_1,…,y_n$,的过程。NMT的一般由Encoder和Decoder,前者学习source sentence的向量化表示,后者是每次生成一个目标单词,故条件概率为:
$$\log p(y|x) = \sum_{j=1}^m \log p(y_j|y_{<j}, \mathbf{s})$$
$\mathbf{s}$ 表示source sentence。encoder和decoder一般使用RNN(GRU/LSTM)来实现。对于预测单词$y_j$,其概率计算可归纳为:
$$p(y_j|y_{<j},\mathbf{s}) = \text{softmax}(g(\textbf{h}_j))$$
softmax是在整个词汇表长度上进行的,$\mathbf{h}_j$是RNN的单元,其计算可归纳为:
$$\mathbf{h_j} = f(h_{j-1},\mathbf{s})$$
$f$可以表示普通RNN单元、GRU或LSTM计算实现。
Global Attention
我们使用$h_s$表示source hidden state(encoder的隐藏层对不同time-step输入的$x_t$的编码结果)。使用 $\bar{h}_t$表示target hidden state(decoder的隐层状态)。Attention的思想是对每个$h_s$设置一个权重 $\mathbf{a}_t(\mathbf{s})$,下标t表示decoder的time-step。假如$h_s$的长度为$n_h$,则我们可以设置$n_h$个权重值:{$a_0^{1}, a_0^2,…, a_0^{n_h}$},每个权重值下标表示decoder的time-step,上标表示对应的source hidden state。权重的计算函数可以记为score(李宏毅中使用match),函数的输入为 $\text{score}(\mathbf{h}_t,\bar{\mathbf{h}_s})$。score函数的实现有多种方式:
$$\text{score}(\mathbf{h}_t,\bar{\mathbf{h}_s}) = \begin{cases}
\mathbf{h}_t^T \bar{\mathbf{h}_s} \qquad\qquad\qquad dot \\
\mathbf{h}_t^T \mathbf{W}_a \bar{\mathbf{h}_s} \qquad\qquad general \\
\mathbf{v}_a^T \text{tanh}[\mathbf{h}_t^T : \bar{\mathbf{h}_s}] \quad concat \\
\end{cases}$$
在得到每个权重后,还需要对其进行softmax:
$$\mathbf{a}_t(\mathbf{s}) = \text{align}(\mathbf{h_t}, \bar{\mathbf{h}}_s)$$
$$=\frac{\exp(\text{score}(\mathbf{h}_t^T,\bar{\mathbf{h}_s}))}{ \sum_s \exp(\mathbf{h}_t^T,\bar{\mathbf{h}_s})}$$
在得到权重的最终值$a_t(s)$后,我们将权重和source hidden state相乘,可以得到向量$c_t$:
$$c_t = \sum a_t(s)\cdot\bar{h}_s$$
最后decoder的最终输出为 $\tilde{\mathbf{h}}_t$:
$$\tilde{\mathbf{h}}_t = \text{tanh}(\mathbf{W}_c[c_t;\mathbf{h}_t])$$
最后经过softmax可以得到预测单词$y_t$:
$$p(y_t|y_{<t}, x) = \text{softmax}(\mathbf{W}_s \tilde{\mathbf{h}_t})$$
Attention层中的$W_a,W_c$是超参数,通过训练学习。
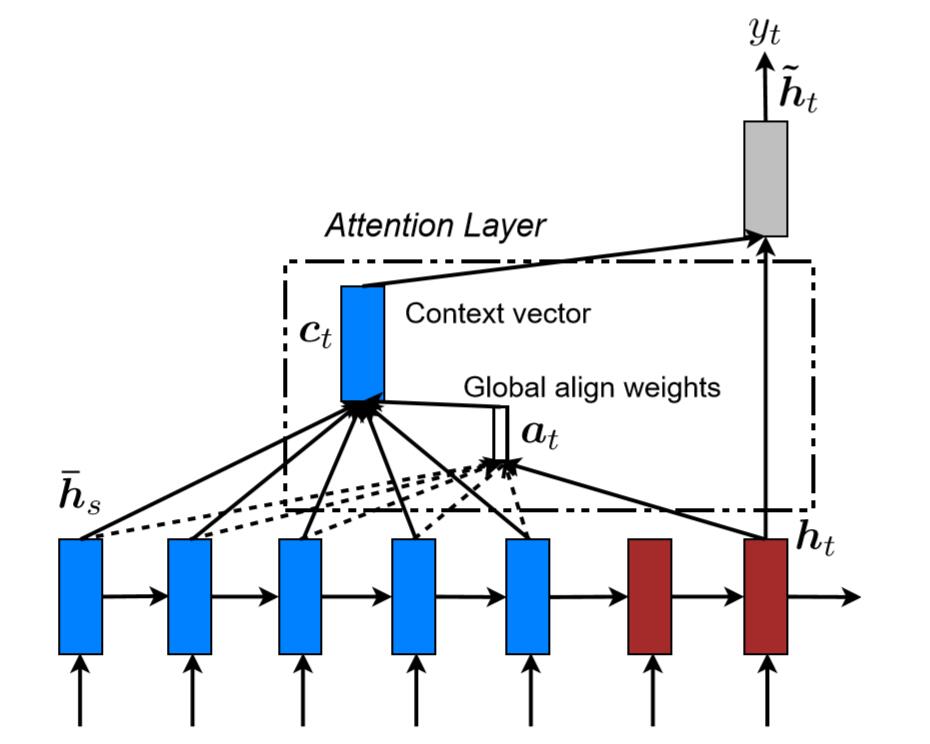
$h_t$与$a_t$的连线为实线,因为对于每一个 $\bar{h}_s$的权重计算都需要使用 $h_t$。而 $\bar{h}_s$是逐个计算的,因此是虚线。$a_t$经过softmax后,与每个source hidden state相乘得到 $c_t$。$c_t$与 $h_t$相乘得到 $\tilde{h}_t$。
Local Attention
Local Attention是受soft/hard attention启发。其思想是当序列过长的时候,将注意力分散到全部的source hidden state并不合适,计算量很大。因此,想缩小attention的范围。根据经验设置一个超参数$D$,对于每次预测的time-step t选择一个position $p_t$。然后在 $[p_t-D , p_t+D]$窗口范围进行Attention。$p_t$的选取有两种:
- Monotonic alignment (local-m):$p_t = t$
- Predictive alignment (local-p):$p_t = S \cdot \text{sigmoid}(v_p^T\text{tanh}(W_p\mathbf{h}_t))$ 当然$a_t(s)$函数也有变动,可详见论文。
总结
论文整体的架构如下图,其中提到了Input-feeding方法。其目的是将每次的attention连续起来,是出于如果每次attention的决策都是独立的情况是不合理的直觉。从这个图可以看出,decoder的输入为 $[h_{t-1},\tilde{h}_t,y_t]$,及上一个隐层状态,上一个输出单词以及attention layer输出的最终decoder状态$\tilde{h}_t$。这里和其它Attention有些不同,后来模型是使用$c_t$替代$\tilde{h}_t$。并且从模型角度讲,$\tilde{h}_t$经过softmax得到输出$y_t$,然后二者同时输入到下一个隐层,感觉有点重复,还没找到相关解答。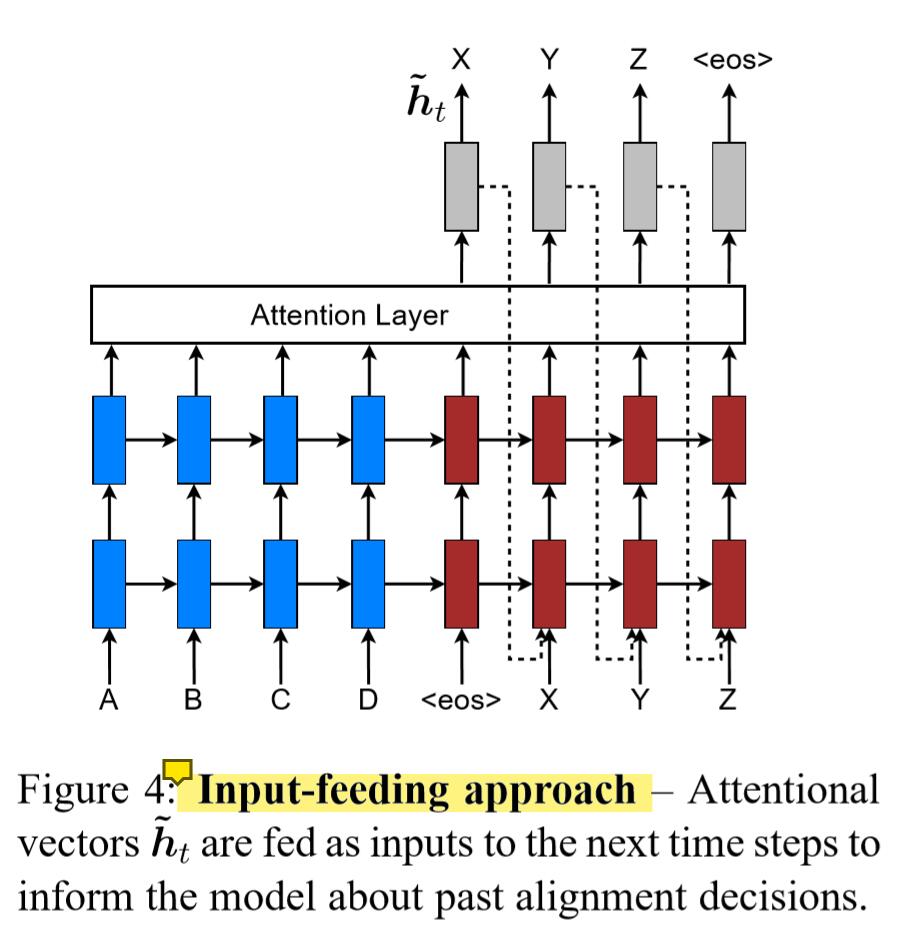
Attention模型之二详解
待更新
BERT模型中的QKV概念
总结一下,attention就是算一个encoder output的加权和,叫做context;计算方法为,query和key计算相关程度,然后归一化得到alignment,即权重;然后用alignment和memory算加权和,得到的向量就是context。
Attention和Transformer