Incrementality in Deterministic Dependency Parsing
Joakim Nivre
Vaxjo University
Abstract
确定性依赖解析(Deterministic dependency parsing)是一个鲁棒和高效的非限制性自然语言文本句法解析方法。本文分析了其增量处理的可能性,并得出结论:在此框架内无法严格实现增量。但是我们还证明,通过选择最优解析算法,可以最小化需要非增量处理结构的数量。这一说法得到了实验证据的证实,该证据表明,当在瑞典文本的随机样本上进行测试时,该算法实现了对输入的68.9%的增量解析。 当限于解析器接受的句子时,增量程度增加到87.9%。
Introduction
增量解析被提倡是出于至少两个不同的原因。第一从实用性上讲,语音识别等实时任务需要对当前输入进行不断的更新的分析。第二从理论上来说,增量解析将解析和认知建模(congnitive modeling)联系在一起。
然而,由于不同的原因,目前大多数最先进的解析方法都不遵循增量性原则。尝试完全消除输入歧义的解析器 - 即完全解析 - 通常首先使用某种动态编程算法来派生包解析林(packed parse forest),然后应用概率自上而下模型以选择最可能的分析(Collins, 1997; Charniak, 2000)。由于第一步是基本不确定的,这似乎至少在严格意义上排除了增量性。与之相反,只对输入消除部分歧义的解析器-即部分解析(partial parsing)-通常是确定的,通过一次输入构建最终分析(Abney, 1991; Daelemans et al., 1999)。但由于它们通常会输出一系列未连接的短语或块,因此不能满足增量性的限制。
最近提出的确定性依赖解析(Deterministic dependency parsing)作为用于语法分析非受限自然语言文本的方法,具有鲁棒性和高效性(Yamada and Matsumoto, 2003; Nivre, 2003)。在某些方面,这种方法可以看作是传统的完整解析和部分解析之间的折衷。本质上,它是一种全解析,其目标是构建一个对输入字符的完整的语法分析,而不是仅仅是确定主要成分。但它和部分解析类似,是具有鲁棒,高效和确定性的。总而言之,这些属性似乎是依赖解析适应于增量处理,尽管有些实现并不满足这些约束。例如,Yamada和Matsumoto(2003)使用多通道自下而上算法,结合支持向量机,其方式不会导致增量处理。
在本文中,我们分析了确定性依赖解析中增量性的约束,并认为严格的增量是不可实现的。 然后,我们分析了Nivre(2003)中提出的算法,并且表明,鉴于先前的结果,该算法从增量性的角度来看是最优的。 最后,我们实验性地评估了算法在实际解析中实现的增量程度。
2 Dependency Parsing
在依赖结构中,每个word token是依赖于最多一个的其它word token,通常称之为它的head或regent。也就是说,依赖结构可以使用有向图(directed graph)来表示。节点node表示word token,边arcs表示依赖关系。此外,边arcs可以标记特定依赖类型。图1为瑞典语句的标记依赖图。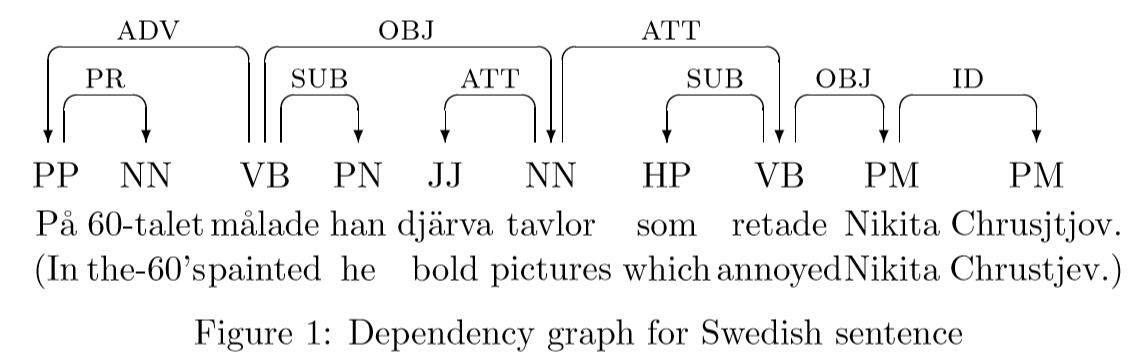
在下文中,我们将注意力限制在未标记的依赖图上,即没有标记弧的图,但结果也将适用于标记的依赖图。 我们也将自己局限于投影依赖图(Mel’cuk,1988)。 在形式上,我们通过以下方式定义这些结构:
一个依赖图的单词集合$W = w_1…w_n$,边集合$D = (W, A)$。A是由边的集合组成,$(w_i, w_j), (w_i, w_j \in W)$。$w_i < w_j$表示$w_i$先于$w_j$在字符串$W$出现。$w_i \rightarrow w_j$ 表示一条边,$\rightarrow^$ 表示弧关系的重新闭合和传递闭合。 $\leftrightarrow$ 和表示 $\leftrightarrow^$ 对应的无向关系。
依赖图 $D = {W, A}$ 的约束如图2。

将字符串$W = w_1…w_n$在满足约束的条件下映射到依赖图的任务,我们称之为依赖解析(dependency parsing)。更多的细节参考Nivre (2003)。
3 Incrementtality in Dependency Parsing
在定义完依赖图后o,我们可以考虑在多大程度上可以逐步构件图。从最严格的意义上讲,我们采用的增量表示,在解析过程中的任何一个时候,都存在一个连接结构,表示目前为止,对输入所做的分析。对我们的依赖图而言,是说在解析过程中图始终是连接的。我们将提高在一分钟内的精度,但首先讨论下增量性(incrementality)和确定性(determinism)间的关系。
至少在从不撤销之前做出的决定这一方面讲,增量性似乎本身并不代表确定性。 因此,涉及回溯的解析方法可以是递增的,只要回溯以这样的方式实现,即我们总是可以维持表示直到回溯点处理的输入的单个结构。 在依赖解析的上下文中,一个典型的例子是Kromann(Kromann,2002)提出的解析方法,它将启发式搜索与不同的修复机制相结合。
在本文中,我们将把注意力限制在依赖性解析的确定性方法上,因为我们认为在更严格的框架内更容易确定基本约束。 我们将以一种方式形式化确定性依赖解析,该方式受传统的基于无上下文语法的shift-reduce解析的启发,使用输入令牌的缓冲区和用于存储先前处理的输入的栈。 但是,由于依赖性解析中不涉及非终结符号,我们还需要维护在处理期间构造的依赖图的表示。
我们使用 $\langle S,I,A \rangle$ 表示解析器配置。$S$是由一个列表表示的栈,$I$ 是输入token列表。$A$ 是依赖图的当前边关系。(由于依赖图的节点由输入字符串给出,因此只需要明确表示弧关系)。给定输入字符串$W$后, 解析器初始化为 $\langle \textbf{nil}, W, \emptyset \rangle$,并在达到 $\langle S, \textbf{nil},A \rangle$条件时终止。如果在结束时图$D=(W,A)$是结构良好的,则接收accept字符串$W$,否则拒绝reject.
为了理解依赖性解析中增量性的约束,我们将首先考虑最直接的解析策略,即从左到右的自下而上解析,在这种情况下,它基本上等同于使用上下文的shift-reduce解析。 乔姆斯基正常形式的自由语法。 解析器以转换系统的形式定义,如图3所示(其中$w_i$和$w_j$是任意字标记):
- Left-Reduce转换是结合了栈里的两个token,$w_i$和$w_j$,通过左向相连:$w_j \rightarrow w_i$,头是$w_j$
- Right-Reduce转换是结合了栈里的两个token,$w_i$和$w_j$,通过右向相连:$w_ \rightarrow w_j$,头是$w_$
- Shift操作是将下一个token进栈。
Left-Reduce和Right-Reduce transitions的约束是保证满足单头Single head条件。Shift操作的约束是列表非空。
可以看到,由于多个transitions能应用相同的配置,整个transition system是不确定的。因此,为了得到具有确定性的解析器,我们需要引入一种解决过渡冲突的机制。不管使用哪个机制,在给定长度为n的字符串下,要保证解析器能在2n transitions内完成。此外,保证解析器生成非循环和映射的依赖图(并且满足单头约束)。 这意味着当且仅当连接时,终止时给出的依赖图是格式良好的。
我们现代可以定义这个框架中解析器的增量的含义。理想情况下,我们希望图表 $\langle W-I,A\rangle$始终连接。 然而,考虑到Left-Reduce和Right-Reduce的定义,不可能在没有将其移动到堆栈的情况下连接新单词,因此似乎更合理的条件是堆栈的大小不应超过2。 通过这种方式,我们要求每个单词一旦被移动到堆栈上就被附加在依赖图中的某处。
我们现在可能会问,是否有可能通过从左到右的自下而上依赖性解析器实现递增性,并且在一般情况下答案结果为“否”。 这可以通过考虑仅包含三个节点的所有可能的投影依赖图并且检查哪些可以递增地解析来证明。 图4显示了相关结构,其中共有七个结构。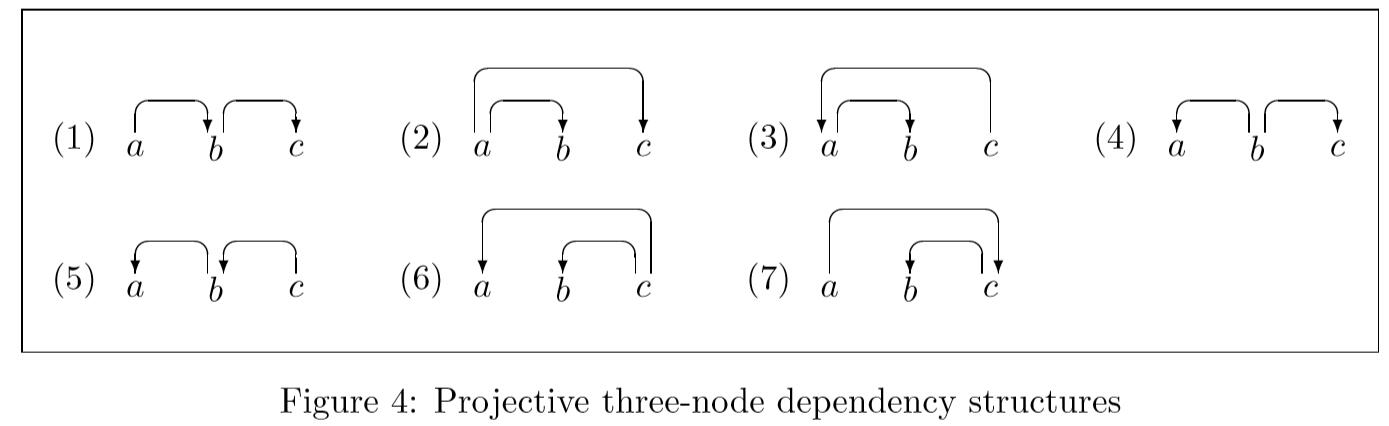
2-5都可以实现结构化增量,首先将两个token进栈,2-3使用Right Reduce, 4-5使用Left Reduce, 之后再都进栈,最后2,4再使用Right Reduce, 3,5 使用Left Reduce。
以(2)为例子,
进栈2个token, statck: [a,b]
使用Right Reduce, 删除b, 产生 $a \rightarrow b$
进栈1个token, stack: [a,c]
使用Right Reduce, 删除c, 产生 $a \rightarrow c$
PS 一般会有个虚拟根节点[ROOT, a, b] 参后
相反,剩下的三个需要先全部进栈才能执行reduction。然而,1和6-7例子解析器不能构成增量解析的原因是不同的。
6-7中前两个节点在最终依赖图中并不是由一条单边连接的。6中前两个全部依赖第三个token.7中巴啦啦拉你懂的。无论使用何种算法,这都必然存在,并且这就是为什么在这里定义的依赖性解析中不可能实现严格的递增性的原因。需要注意的是,作为6-7的镜像2-3,虽然它们包含三个未通过单边相连的相邻token,但它们仍然可以增量解析。原因在于,前两个token的reduction使得第一个与第三个相邻。因此,有问题的结构定义特征是恰好最左的token不直接相连。
1的情况不同之处在于,这是由严格的自下而上的策略引起的,这需要每个token在与其头部结合时要找到其所有的依赖。对于左依赖来说,这没有问题,如5中可以使用Shift和Left-Reduce来交替处理。但在1中,必须从右到左开始。这派出了严格的增量。然而6-7在当前框架中永远不能处理,而1可以修改策略来达到解析。下一节中说明。
在这一点上,与基于扩展分类语法的增量解析进行比较是有益的,其中(6-7)中的结构通常由某种级联(或产品)处理,这与任何真正的语义都不对应。 组成部分的组合(Steedman,2000; Morrill,2000)。 相反,(1)中的结构通常由函数组合处理,其对应于良好定义的组合语义操作。 因此,可能有人认为(6-7)的处理只是伪增量,即使在其他框架中也是如此。
在我们采用严格的自下而上方法之前,可以注意到本节中描述的算法本质上是Yamada和Matsumoto(2003)与支持向量机结合使用的算法,不同之处在于它们允许解析以多个方式执行 传递,其中一次传递产生的图形作为下一次传递的输入.1它们为多次传递解析的主要动机正是自下而上策略要求每个令牌在组合之前找到所有依赖项的事实 用它的头,这也是阻止增量解析结构的原因,如(1)。
4 Arc-Eager Dependency Parsing
为了增加确定性依赖解析的递增性,我们需要结合自下而上和自上而下的处理。 更确切地说,我们需要自上而下处理左依赖者自下而上和右依赖者。 通过这种方式,只要相应的头部和从属关系可用,就会将弧添加到依赖关系图中,即使依赖关系对于其自己的依赖关系是不完整的。 在Abney和Johnson(1991)之后,我们将这种热切的解析称为与前一节中讨论的标准自下而上策略区别开来。
使用与以前相同的解析器配置表示,可以通过图5中给出的转换来定义arc-eager算法,其中wi和wj是任意字标记(Nivre,2003):
- Left-Arc transition:$w_j \overset{r}{\rightarrow} w_i$,含义是,将下一个输入token $w_j$指向栈顶元素$w_i$并出栈(pop stack)
- Right-Arc transition:$w_i \overset{r}{\rightarrow} w_j$,含义是,将栈顶元素$w_i$并出栈(pop stack)指向下一个输入token $w_j$,并将$w_j$入栈
- Reduce transition 出栈(pop stack)
- Shift(SH) 将下一个输入token进栈
可以看出,Left-Arc 和 Right-Arc 类似于 Right-Reduce 和 Right-Reduce。它们确保满足单头(Single head)约束,而只当栈顶token有头时候才能使用Reduce trainsition. Shift与之前一样,列表不为空就可以执行。
比较两个算法,Left-Arc 和 Left-Reduce是对应的,但不同在于,出于对称原因,前者适用于栈顶元素token和下一个输入元素token而不是栈顶的两个元素token。但 Right-Reduce 和 Right-Reduce相比,前者并不减少(Reduce)元素而是简单的将新的右依赖项转移(shift)到栈顶,从而使依赖项可以有自己的右依赖项。但是为了允许多个多个右依赖项,必须还有一种机制来弹出栈中的依赖项。这就是 Reduce transition. 因此,我们可以说,标准自下而上算法中右Reduce transitions所执行的动作是通过Right-Arc结合弧激发(arc-eager)算法中的后续Reduce转换来执行的。由于Right-Arc和Reduce可以由任意数量的转换分隔,因此允许对任意长的右依赖链进行增量解析。对于Arc-eager算法而言,定义增量对于标准自下而上算法来说不那么简单。 简单地考虑堆栈的大小将不再起作用,因为堆栈现在可以包含形成依赖图的连接组件的token序列。另外,由于不再必须转移两个tokens组合到栈,并且因为出栈的任意token都可连接到栈的某个token,我们需要保证图 $(S,As)$ 是一直连接的。$As$表示$A$到$S$的约束,如: $As = {(w_i,w_j) \in A | w_i,w_j \in S }$
给定增量性的定义后,图4中的2-5可以很好使用arc-eager算法的逐步解析,和标准的自下而上算法一样。
$$
\langle \textbf{nil}, abc, \emptyset \rangle \
\downarrow \textbf{Shift} \
\langle a,bc, \emptyset \rangle \
\downarrow \textbf{Right-Arc} \
\langle bc,a,{(a,b)} \rangle \
\downarrow \textbf{Right-Arc} \
\langle cba,\textbf{nil}, {(a,b), (b,c)} \rangle
$$
我们得出结论,相对于依赖性解析中的递增性,arc-eager算法是最优的,即使它仍然适用于图4中的结构(6-7)不能以递增方式解析。接下来的问题是,在实际的解析过程中,出现这样结构的情况有多频繁。这个问题相当于说,Arc-eager算法对严格的增量处理偏离有多少。答案显然取决于选取的语言和理论框架,我们将在下一节来至少谈一谈这个问题。在此之前,我们希望结果能与之前的上下文(context-free)解析联系起来。
首先可以知道,相比于其它context-free解析的标准应用,自下而上和自上而下的术语在依赖解析的上下文中有一点不同的含义。由于依赖图中没有终止节点,自上而下结构表示头节点是在其依赖被绑定前进行绑定的。然而,依赖图中的自上而下结构并不包含从高层节点prediction底层节点,因为所有的节点是输入字符串给定的。因此,就驱动解析过程的因素而言,这里讨论的所有算法都对应于无上下文解析中的自下而上算法。 有趣的是,如果我们将依赖解析的问题重新定义为使用CNF语法的无上下文解析,那么图4中的有问题的结构(1),(6-7)都对应于右分支结构,并且很好 - 已知自下而上的解析器可能需要无限量的内存来处理右分支结构(Miller和Chomsky,1963; Abney和Johnson,1991)。
此外,如果我们在Abney和Johnson(1991)的框架下分析这里讨论的两种算法,它们对于枚举节点的顺序完全不同,而只是对枚举的顺序有所不同;第一种算法是电弧标准,而第二种算法是弧形标准。 Abney和Johnson(1991)提出的观察之一是,无弧上传解析的弧形策略有时可能需要比弧标准策略更少的空间,尽管它们可能会导致局部模糊性的增加。看起来关于图4中结构(1)的依赖关系解析的arc-eager策略的优点可以沿着相同的行解释,尽管依赖图中缺少非终结节点意味着本地没有相应的增加歧义。虽然详细讨论无上下文解析和依赖解析之间的关系超出了本文的范围,但我们推测这可能是依赖表示在解析中的真正优势。
5 Experimental Evaluation
结果可以在表1中找到,我们看到在解析613个句子(平均长度为14.0个单词)中使用的16545个配置中,68.9%在堆栈上有零个或一个连接组件,这是我们要求的 一个严格的增量解析器。 我们还发现,大多数违反增量的行为相当温和,因为超过90%的配置在堆栈上的连接组件不超过三个。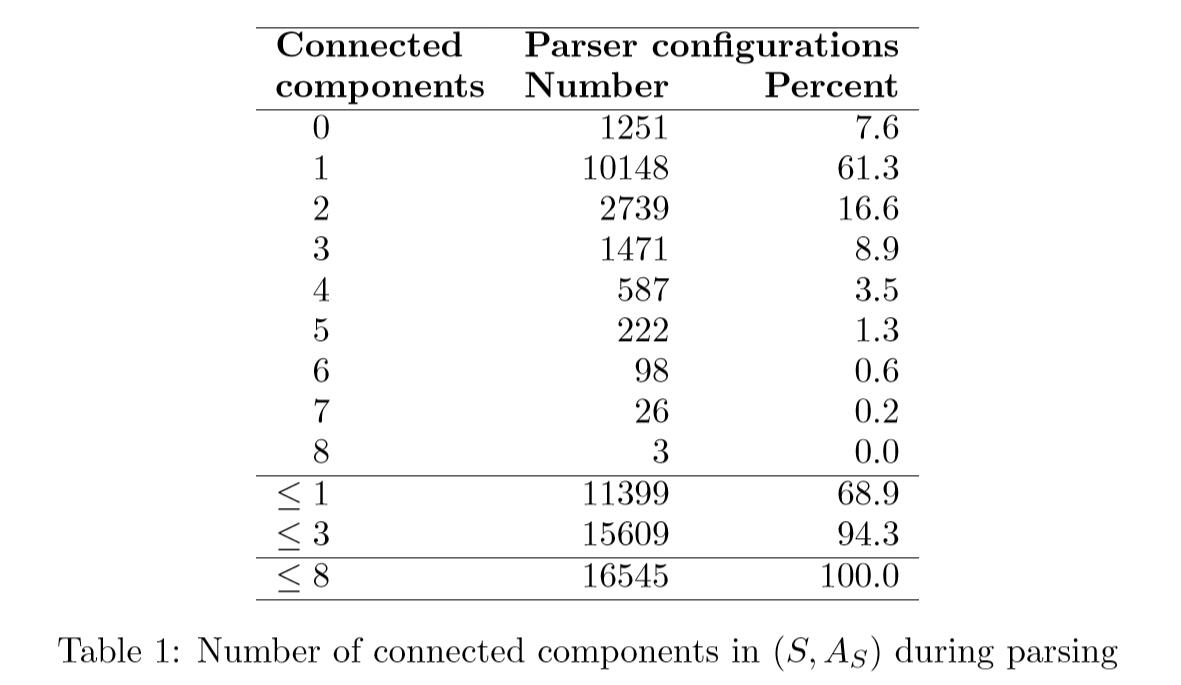
许多违反增量的行为是由无法解析为良好的依赖图的句子引起的,即单个映射依赖树,但解析器的输出是一组内部连接的组件。 为了测试不完全解析对增量统计的影响,我们进行了第二个实验,其中我们将测试数据限制为444个句子(613个中),本文生成了一个格式良好的依赖图。 结果可以在表2中看到。在这种情况下,87.1%的配置实际上满足增量性的约束,并且堆栈中具有不超过三个连接组件的配置的比例高达99.5%。
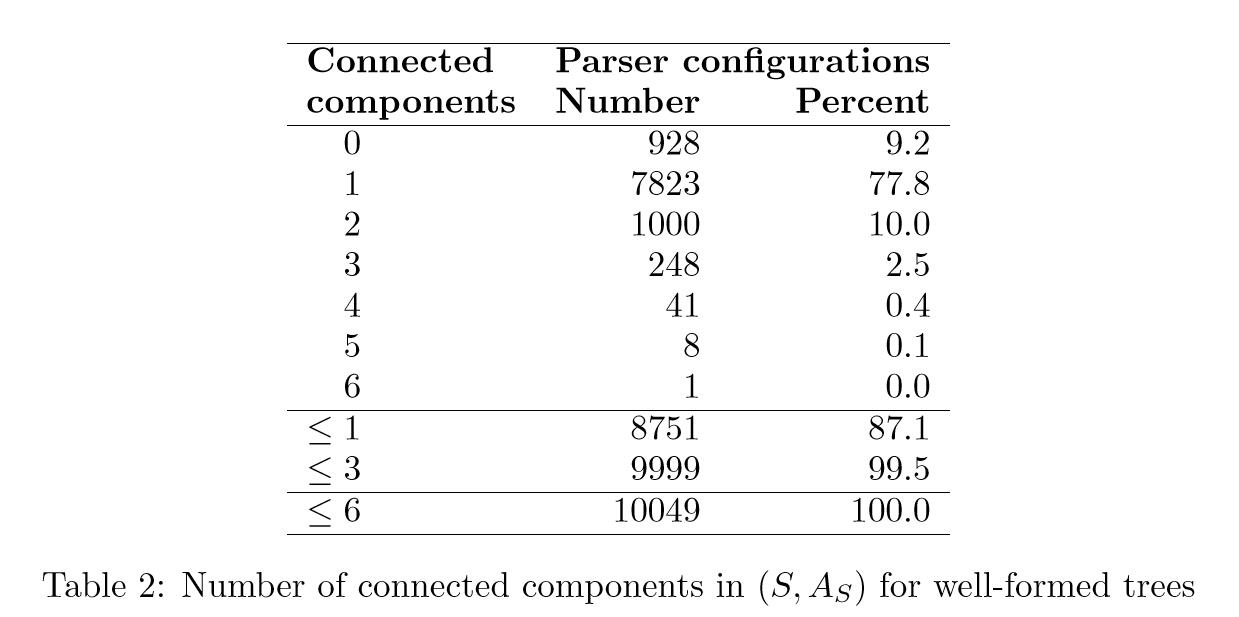
似乎可以得出结论,尽管在确定性依赖性解析中不可能采用严格的逐字增量,但实际上,Arc-eager算法可以被视为增量解析的近似近似。
6 Conclusion
本文分析了确定性依赖解析的增量性实现的可能。我们的第一个结果是否定的,因为我们已经证明在这里考虑的限制性解析框架中无法实现严格的增量。然而,我们证明对于增量依赖解析器,考虑到所有的框架约束,arc-eager解析算法是最优的。此外,我们已经表明,在实际解析中,算法对大多数输入结构执行增量处理。如果我们考虑测试数据中的所有句子,则占比大约为三分之二,但如果我们将注意力限制在格式良好的输出上,则几乎为90%。 由于先前已经证明确定性依赖性解析在解析准确性方面具有竞争力(Yamada和Matsumoto,2003; Nivre等,2004),我们认为这个有前景的方法是适应于具有鲁棒性,高效性及(近乎)增量性的需求的。