04.卷积神经网络
00? 动态性策略如何与DL结合(预测之上的决策系统)?
第一周 卷积神经网络
1.1 计算机视觉 (Computer vision)
将CV知识应用到新的领域,催生新的网络结构
目标检测 风格迁移
一个64x64的图像,会有12288个维度,
一个1000x1000的图像,会有3M个维度,
假如第一层神经元有1000个,则$w^{[1]}$有3B个参数,这太大了!
故需要卷积
1.2 边缘检测示例 (Edge detection example)
*是卷积操作的标准符号
对卷积不了解可详细看这个视频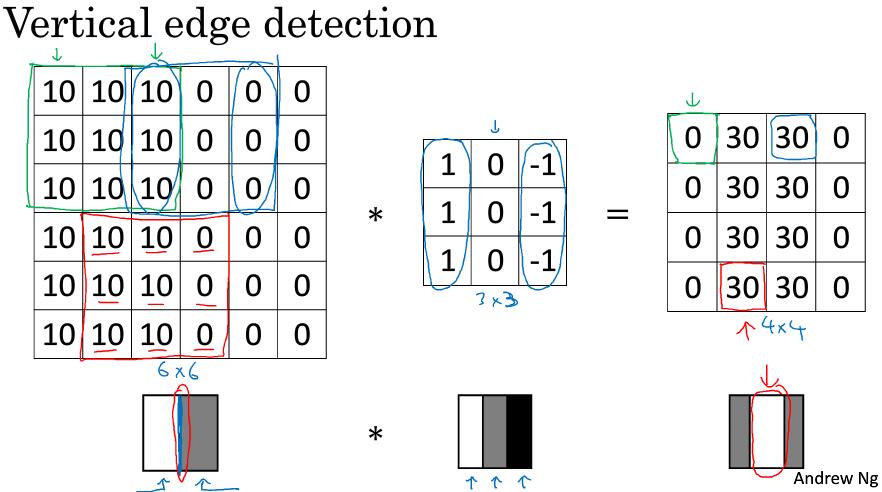
参考论文
1.3 更多边缘检测内容 (More edge detection)
固定的卷积核:
Sober过滤器:
| - | - | - |
|---|---|---|
| 1 | 0 | -1 |
| 2 | 0 | -2 |
| 1 | 0 | -1 |
Scharr过滤器:
| - | - | - |
|---|---|---|
| 10 | 0 | -3 |
| 10 | 0 | -10 |
| 3 | 0 | -3 |
另一种思想:将9个数字作为参数进行学习,是CV的有效思想之一。
1.4 Padding
普通的卷积操作
- 输出减少,$output: (n-k)+1$,输出图片变小
- 丢失了图像边缘的大部分信息
对原始图片进行填充,如用0填充,则输出(n+2p-k)+1=6,图像保持不变。
Valid convolution:不使用填充,$n\times n * f\times f \rightarrow (n-f+1) \times (n-f+1)$
Same convolution:使用填充,保持图片大小不变。$n+2p-f+1 \times n+2p-f+1$ 继续求解可得$p = \frac{f-1}{2}$
卷积核一般为奇数
1.5 卷积步长 (Strided convolution)
输出图片维度(向下取整):$\lfloor \frac{n+2p-f}{s}+1 \rfloor$
按机器学习惯例,不使用翻转操作,技术上讲,可能叫互相关更好,深度学习中叫做卷积操作。
1.6 三维卷积 (Convolutions over volumes)
输出:$n\times n \times n_c * f\times f \times n_c \rightarrow n-f+1 \times n-f+1 \times n_c’$
$n_c$是channel, $n_c’$是卷积核的数量
1.7 单卷积层网络 (One layer of convolution network)
假如有10个3x3x3的卷积核,则该层的参数为280个。而无论你的输入的图片大小是多少,参数个数是不变的,即使用10个特征提取。卷积之后得到feature_map,与偏置项$b$相加,得到$z^{[l]}$,然后再应用激活函数得到$a^{[l]}$

$f^{[l]}$是卷积核的大小,$n_c^{[l]}$是卷积核的个数
$p^{[l]}$是padding, $s^{[l]}$是步长
输入为上一层的输出,所以为$n_H^{[l-1]} \times n_w^{[l-1]} \times n_c^{[l-1]}$
卷积计算:$n_H^{[l]} = \frac{n_H^{[l-1]}+2p^{[l]}-f^{l}}{s^{[l]}} + 1$,同理$n_w^{[l]}的计算$
每一个卷积核(过滤器)维度:$f^{[l]} \times f^{[l]} \times n_c^{[l-1]} $,$n_c^{[l-1]}$是上一层输出的channel。
激活函数:$a^{[l]} = n_H^{[l]} \times n_W^{[l]} \times n_c^{[l]}$
权重Weights:$f^{[l]} \times f^{[l]} \times n_c^{[l-1]} \times n_c^{[l]}$,$n_c^{[l]}$是卷积核的个数
偏置项bias:$n_c^{[l]}\rightarrow(1,1,1,n_c^{[l]})$
1.8 简单卷积网络示例 (A simple convolution network example)
假设输入图片大小:$n_{H}^{[0]} = n_{W}^{[0]}=39$,$n_{c}^{[0]} =3$
第一层卷积:10个$f^{[1]} = 3$,$s^{[1]} = 1$,$p^{[1]} =0$,则$a^{[1]}=$37×37×10
第二层卷积:20个$f^{\left\lbrack 2 \right\rbrack}=5$,$s^{\left\lbrack 2 \right\rbrack}=2$,$p^{\left\lbrack 2 \right\rbrack} = 0$,则$a^{\left\lbrack 2 \right\rbrack}=$17x17x20
第三层卷积:40个$f^{\left\lbrack 3 \right\rbrack}=5$,$s^{\left\lbrack 3 \right\rbrack}=2$,$p^{\left\lbrack 3 \right\rbrack} = 0$,则$a^{\left\lbrack 3 \right\rbrack}=$7x7x40=1960
最后处理成向量,接softmax或logistic回归函数
典型的卷积神经网络层:
- Convolution (Conv)
- Pooling (POOL)
- Fully connected (FC)
1.9 池化层 (Pooling layers)
Max pooling:如果在卷积核中提取到某个特征,则保留其最大值,如果没有提取到,最大值也很小。仅是直观理解,但实验效果良好。步长和大小不需要学习。p一般为0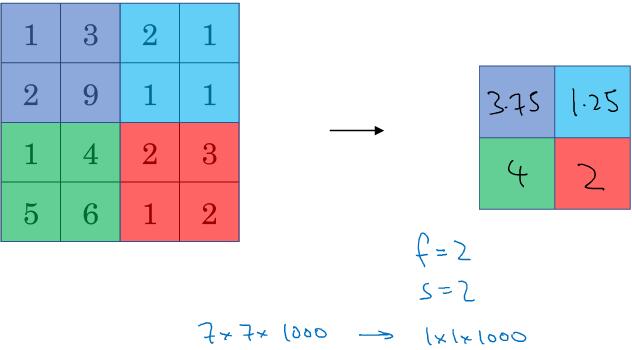
Average pooling:不太常用。
1.10 卷积神经网络示例(Convolutional neural network example)
类似于Le-Net-5
逐步讲解各卷积层的输出维度
有的文献将卷积和池化作为一层神经网络。
随着网络的加深,高度$n_{H}$和宽度$n_{W}$通常都会减少,而通道数量会增加。
在神经网络中,另一种常见模式就是一个或多个卷积后面跟随一个池化层,然后一个或多个卷积层后面再跟一个池化层,然后是几个全连接层,最后是一个softmax。这是神经网络的另一种常见模式。

有几点要注意,第一,池化层和最大池化层没有参数;第二卷积层的参数相对较少,前面课上我们提到过,其实许多参数都存在于神经网络的全连接层。观察可发现,随着神经网络的加深,激活值尺寸会逐渐变小,如果激活值尺寸下降太快,也会影响神经网络性能。示例中,激活值尺寸在第一层为6000,然后减少到1600,慢慢减少到84,最后输出softmax结果。我们发现,许多卷积网络都具有这些属性,模式上也相似。
1.11 为什么使用卷积神经网络 (Why convolutions?)
卷积神经网络的优点:
- 参数共享:特征检测如垂直边缘检测如果适用于图片的某个区域,那么它也可能适用于图片的其他区域,共享特征选择器。
- 稀疏连接:如32x32x3 = 3072 使用6个5核卷积得到28x28x6=4704,如果用传统的全连接则需要3072x4704=14M参数,而卷积只需要(5x5+1)x6=156个参数。同时,映射后的feature_map某一像素点只和整张图片中的25个像素点有关联,所以是稀疏连接。
Parameter sharing: A feature detector (such as a vertical edge detector) that’s useful on one part of the image is probably useful in another part of the image.
Sparsity of connections: In each layer, each output value depends only on a small number of inputs.
卷积网络可以使用任何的代价函数$J$,以及其它梯度下降算法(Momentum,RMSprop,Adam)
第一周作业
卷积神经网络的反向传播
第二周 深度卷积网络:实例探究 (Deep convolutional models: case studies)
2.1 为什么要进行实例探究 (Why look at case studies?)
通过他人案例学习建立卷积神经网络的直觉与技巧。
尝试读计算机视觉(CV)论文
提纲:
- 经典网络
- LeNet-5 1980
- AlexNet
- VGG
- ResNet 训练了深达152层的网络
- Inception
2.2 经典网络 (Classic networks)
LeNet-5 离线阅读
论文发表于1998年,当时使用的平均池化,也没有采用padding。LeNet-5在全连接最后一层使用的不是softmax,而是另一种,现在很少用到的分类器。此外,当时使用的激活函数为Sigmoid和tanh,而不是ReLu。PPT内容大部分来自于论文II和III,精读第II段,泛读第III段。AlexNet 离线阅读
AlexNet使用227x227x3(原文使用224x224x3)图片作为输入,部分卷积层使用了padding,还是用了复杂的GPU计算,激活函数选取的ReLu,最后一层使用softmax,同时使用了局部响应归一化层”(Local Response Normalization),即LRN层,LRN效果没多大作用。VGG-16
VGG-16 虽然包含16个看似很多的的网络层,但结构并不复杂。首先卷积核(过滤器)的数量,64-128-256-512-512。
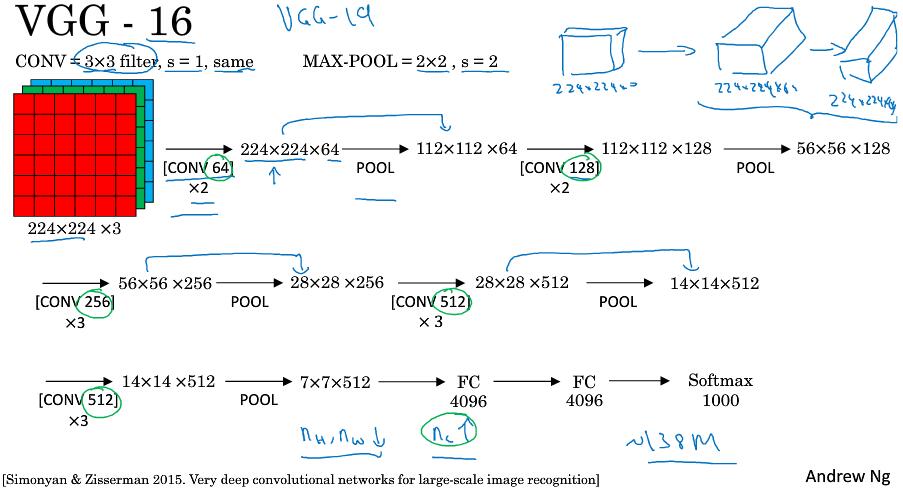
如果你对这些论文感兴趣,我建议从介绍AlexNet的论文开始,然后就是VGG的论文,最后是LeNet的论文。虽然有些晦涩难懂,但对于了解这些网络结构很有帮助。
2.3 残差网络 (Residual Networks (ResNets))
ResNet论文中将逐层传播网络定义为plain network,而ResNet的不同就是添加了”short cut/skip connection”,形成了Residual block。示意图: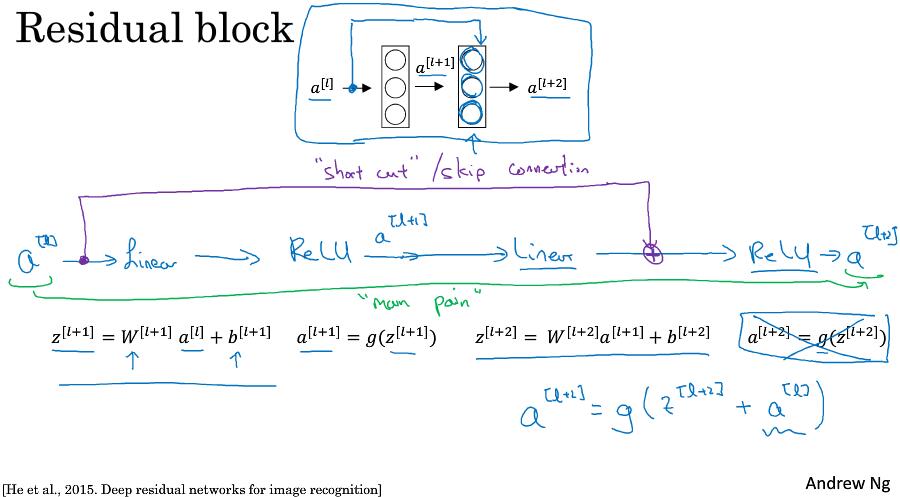
在第二层线性变化后,非线性激活前,添加一样$a^{[l]}$,即$a^{[l+1]} = g(z^{[l+1]} + a^{[l]})$
整个网络示意图: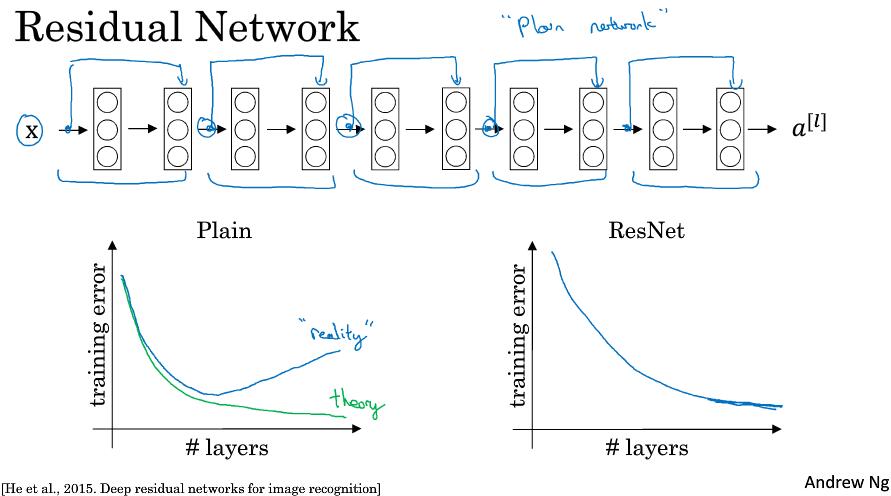
残差网络解决了梯度消失或爆炸,允许网络结构更加深层。
残差网络为什么有效 (Why ResNet work)
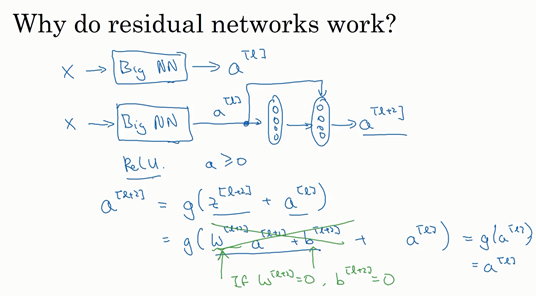
设想一个神经网络的输出为$a^{\left\lbrack l \right\rbrack}$, 我们在它后面添加带“residual block”的两层网络。此时,$a^{\left\lbrack l + 2\right\rbrack} = g(z^{\left\lbrack l + 2 \right\rbrack} + a^{\left\lbrack l\right\rbrack})$。如果使用L2正则化,那么权重$W^{[l+1]}$会被压缩,$b$偶尔也会被压缩,注意$W$,如果$W^{\left\lbrack l + 2 \right\rbrack} = 0$,为方便起见,假设$b^{\left\lbrack l + 2 \right\rbrack} = 0$,这几项就没有了,因为它们($W^{\left\lbrack l + 2 \right\rbrack}a^{\left\lbrack l + 1 \right\rbrack} + b^{\left\lbrack l + 2\right\rbrack}$)的值为0。最后$ a^{\left\lbrack l + 2 \right\rbrack} = \ g\left( a^{[l]} \right) = a^{\left\lbrack l\right\rbrack}$,因为我们假定使用ReLU激活函数,并且所有激活值都是非负的,$g\left(a^{[l]} \right)$是应用于非负数的ReLU函数,所以$a^{[l+2]} =a^{[l]}$。
事实上,残差块学习这个恒等式函数并不难。从上面可以看出,即使网络添加了两层,但它的效率比没有降低,所以将残差块放到网络中间还是末尾,都不影响网络。
此外,如果这些隐层能学到一些拥有东西,比恒等式表现还好,那网络可以提升效果,或者说至少不会降低。
一个细节:ResNets使用了需要SAME卷积,保证了$a^{\left\lbrack l\right\rbrack}$与残差块的维度一致,当不一致的时候,在残差块中添加一个科学系参数$W_s$,即$a^{\left\lbrack l + 2\right\rbrack} = g(z^{\left\lbrack l + 2 \right\rbrack} + W_s \cdot a^{\left\lbrack l\right\rbrack})$
论文中,使用卷积-卷积-卷积-池化 -卷积-卷积-卷积-池化….最后使用softmax
2.5 网络中的网络以及1x1卷积 (Network in Network and 1x1 convolutions)
对于通道为1的6x6图片,使用1x1卷积核似乎作用并不大,仅仅是对二维数组进行了扩大或缩放。
但对于通道为32的6x6输入来说就不一样了,这时候我们使用一个1x1的卷积核(实际维度为1x1x32,卷积核通道与输入通道一致)。这时候的卷积操作,是将输入中的一个1x1x32的切片,乘以1x1的卷积核中32个不同的权重再求和,最后应用ReLU激活函数。当然这是1个卷积核,如果是32个卷积核,则效果如下: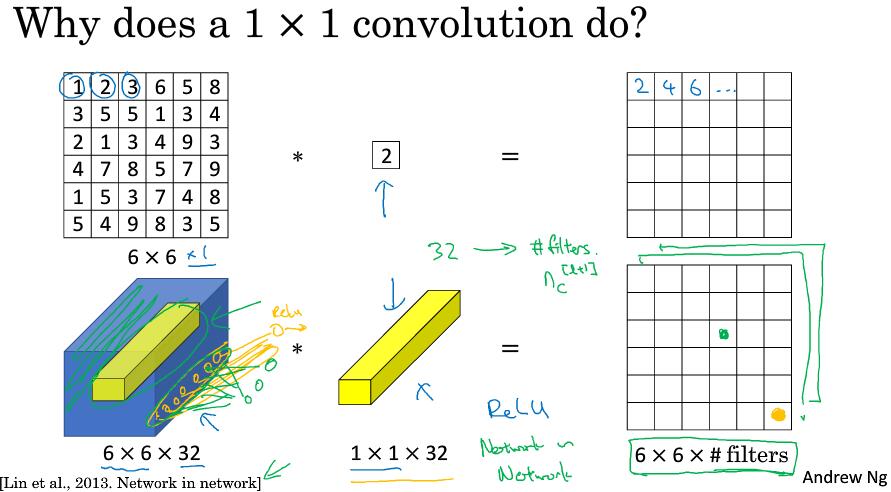
这种方法通常称为1×1卷积,有时也被称为Network in Network,在林敏、陈强和杨学成的论文中有详细描述。虽然论文中关于架构的详细内容并没有得到广泛应用,但是1×1卷积或Network in Network这种理念却很有影响力,很多神经网络架构都受到它的影响,包括下节课要讲的Inception网络。
这时候输入输出的通道数量保持一致,因此改变卷积核的数量可以进行通道的压缩与扩充(池化仅仅压缩图片的高和宽)
2.6 Google Inception network 简介
Inception层或Inception网络可以用来代替人工来确定卷积层中的过滤器类型(1x1?3x2?5x5?)。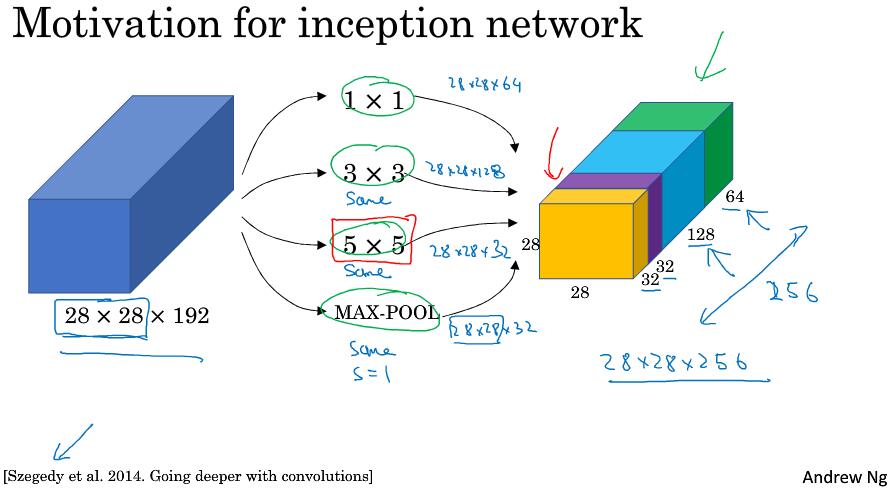
从图中可以发现会设计大量的计算,我们先来看一下5x5的卷积计算成本。
对于28x28x192的输入,采用32个5x5(x192)的卷积进行操作,计算量为 28x28x32 x 5x5x192 = 120M(120422400)
32个核 每个核参数为 5x5x192 做一次卷积需要的stride为 28x28 所以计算成本为 32x5x5x192x28x28
而考虑下面的结构: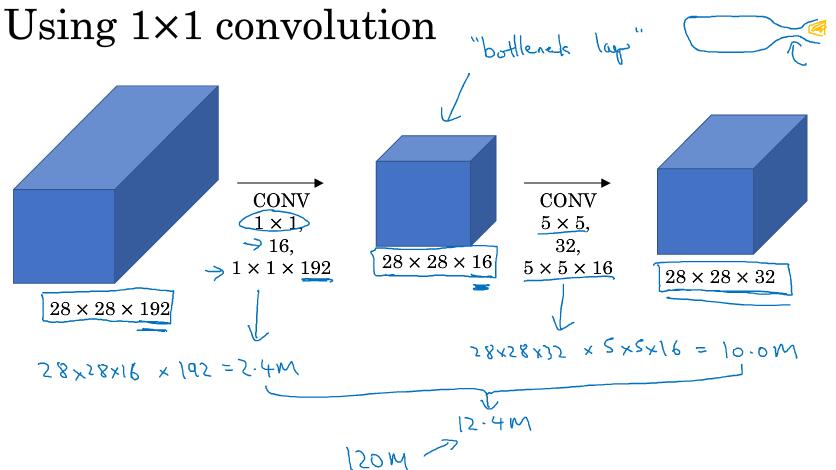
对于28x28x192的输入,我们想要得到和之前一样的输出维度28x28x32,先使用16个1x1(x192)的核卷积,再使用32个5x5(x16)的核卷积。其计算量为 28x28x16 x 192 = 2.4M 28x28x32 x 5x5x16=10.0M,总计为12.4M,与上面的结果相比,缩小了10倍。
所以$ 1\times1 $卷积核作为“bottleneck layer”的过渡层能够有效减小卷积神经网的计算成本。事实证明,只要合理地设置“bottleneck layer”,既可以显著减小上层的规模,同时又能降低计算成本,从而不会影响网络的性能。
2.7 Inception 网络
通过计算成本的对比,可以发现使用1x1的卷积核能够简化计算量,因此可以构建Inception module: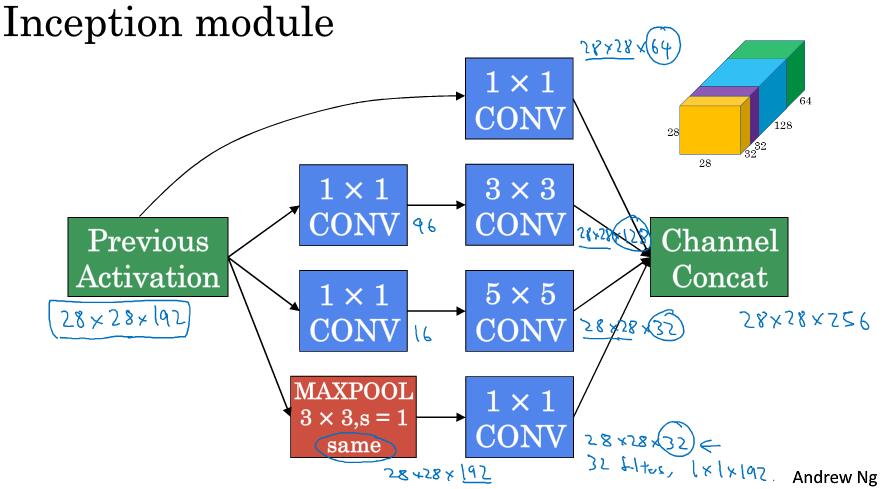
有了Inception module,则Google的gooLeNet网络就很好理解了: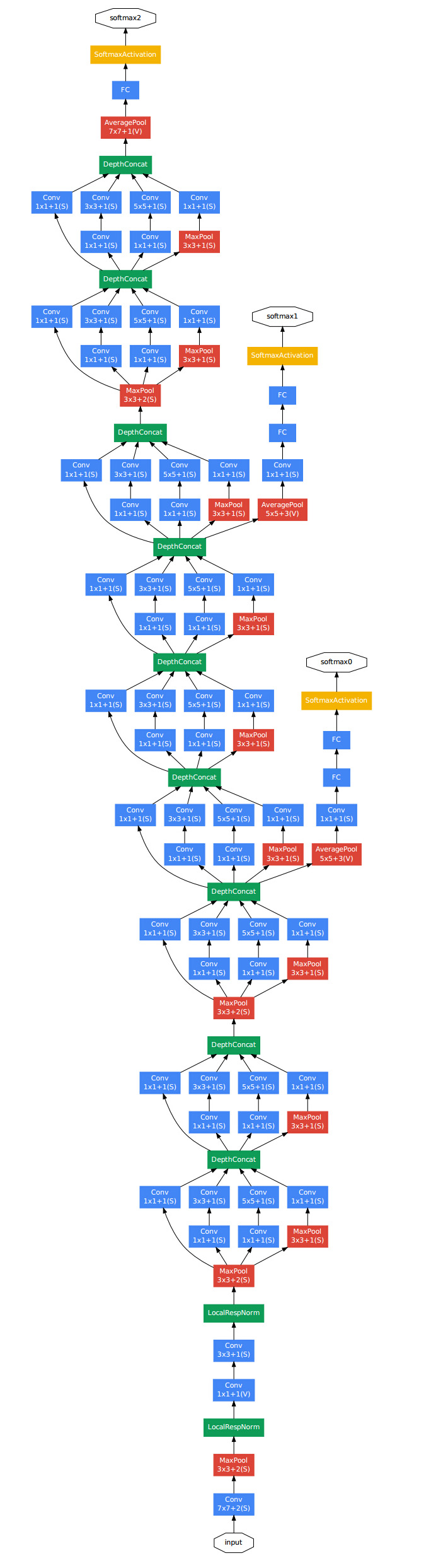
该模型使用多个Inception Module,此外模型多两个softmax输出,能对网络进行调整,并防止过拟合。Inception网络还有很多新版本,如Inception V2、V3以及V4,还有一个版本引入了跳跃连接(skip connection)的方法,有时也会有特别好的效果。
2.8 使用开源的实现方案 (Using open-source implementations)
熟练使用GitHub,如REstNets实现
2.9 卷积网络的迁移学习 (Transfer Learning)
如果建立自己的CV检测器,可以下载神经网络的开源实现,不仅包括代码,还包括权重。这样,修改最后一层的softmax层,freeze前面的神经网络,然后在你的数据集上进行训练。
一个经验是,你的数据量越大,你需要freeze的层数越小,甚至仅仅把它们来当作初始化参数。CV中,迁移学习是很值得考虑去做的。
2.10 数据增强 (Data argumentation)
数据扩充方式:
- 镜像(Mirroring)
- 随机裁剪(Random Cropping)
- 其它实现比较复杂的方式:旋转,扭曲,
- 色彩转换,使用PCA颜色增强(AlexNet有细节,也有其它开源实现)
CPU并行:几个线程或进程做数据增强,其它CPU或GPU训练网络。
2.11 计算机视觉现状 (The state of computer vision)
语音识别、图像识别、目标检测任务现所有的数据一个比一个少。数据越少的任务可能越需要手工工程。
在机器学习应用时,学习算法有两种知识来源。
- Labeled data
- Hand engineered features / network architecture / other components
在缺乏数据的情况下,获取良好的表现方式还是花更多时间进行架构设计,或者在网络架构上花费更多时间。
Benchmark 基准测试,Benchmark是一个评价方式,在整个计算机领域有着长期的应用。维基百科上解释:“As computer architecture advanced, it became more difficult to compare the performance of various computer systems simply by looking at their specifications.Therefore, tests were developed that allowed comparison of different architectures.”Benchmark在计算机领域应用最成功的就是性能测试,主要测试负载的执行时间、传输速度、吞吐量、资源占用率等。
在基准/竞赛中提升效果
- 集成 Ensembling
- Train several networks independently and average their outputs
- 多折验证 Muti-crop at test time
- Run classifier on multiple versions of test images and average results
集成大概可以提高1%或2%,但消耗时间。
Muti-crop 是说将你的测试图片进行多次裁剪,每张都进行预测,然后综合考虑结果。
这两种方式在实际生产情况下,很少考虑,在基准测试和竞赛上做得很好。
最后,其他人可能已经在几路GPU上花了几个星期的时间来训练一个模型,训练超过一百万张图片,所以通过使用其他人的预先训练得模型,然后在数据集上进行微调,你可以在应用程序上运行得更快。当然如果你有电脑资源并且有意愿,我不会阻止你从头开始训练你自己的网络。事实上,如果你想发明你自己的计算机视觉算法,这可能是你必须要做的。
第三周 目标检测
3.1 目标定位
识别一张图片中是否有车的分类问题已经很熟悉了,现在还要输出车在图片中的位置,即定位分类问题Classification with Location。进一步,如果图片中包含多个物体需要定位,就是目标检测。
例:识别一张图片是1 行人 2 汽车 3 自行车 4 背景 类别。首先记图像左上角为(0,0),右下角记(1,1)。图像的边框用bx,by,bh,bw来表示中心坐标点和宽高。这时候神经网络的输出向量可以定义为$[P_c,bx,by,bh,bw,c1,c2,c3]$。$pc$表示是前三类与否,如果为1,则$bx,by,bh,bw$来表示坐标,$c1,c2,c3$来表示具体的某一类。
此外,损失函数也需要修改:
$$L(\hat{y},y)=\begin{cases}
\sum_i(\hat{y}_i-y_i)^2& \text{if} \ y_1=1\\
(\hat{y}_1-y_1)^2& \text{if} \ y_1=0\
\end{cases}$$
实际中,可以不对$c_{1}$、$c_{2}$、$c_{3}$和softmax激活函数应用对数损失函数,并输出其中一个元素值,通常做法是对边界框坐标应用平方差或类似方法,对$p_{c}$应用逻辑回归函数,甚至采用平方预测误差也是可以的。
3.2 特征点检测 (Landmark detection)
如果需要检测64个人脸关键点,则可以使卷积神经网络输出为129个,第一个代表有无人脸,剩余的表示各个特征的坐标。
3.3 目标检测 (Object detection)
使用卷积神经网络进行对象检测,采用是基于滑动窗口的目标检测算法。
选用不同的窗口和步长会有一定的影响,太小计算量大,太大影响效果。
不过计算成本得到了解决,见下。
3.4 卷积的滑动窗口实现 (Convolutional implementation of sliding windows)
之前讲的滑动检测计算效率太低,其中一个原始是因为重复计算问题。
而现在,不需要将图片每次切割单独放入神经网络去计算,可是将卷积神经网络的最后全连接层也改用为卷积层。输入也只需要输入原图片完整一次。
改写全连接层:
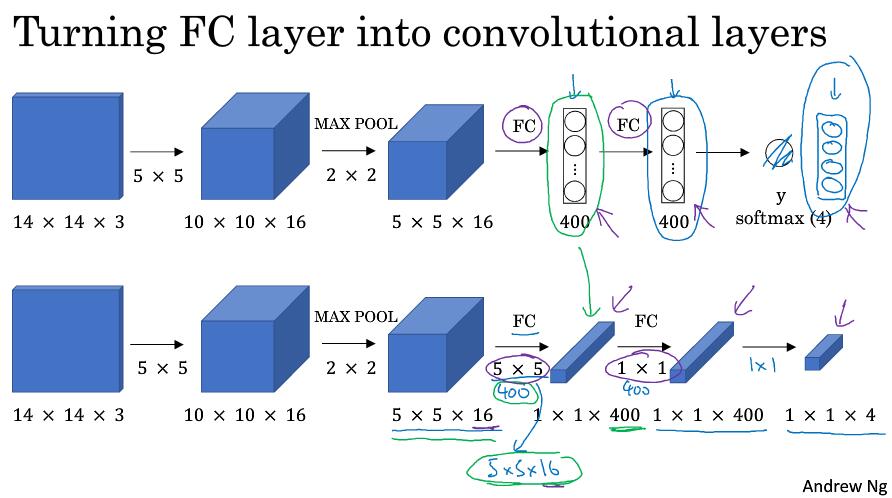
假如输入图片是14x14x3,经过16的5x5卷积得到10x10x16,再经过池化得到5x5x16。连接两个400个节点的全连接层,输出四分类向量。
改写成卷积层:
前面一致,得到5x5x16特征后使用400个5x5的窗口可以得到1x1x400向量,再使用400个1x1的窗口,可以得到1x1x400向量,最后使用1x1的窗口可以得到1x1x4的向量。一次计算
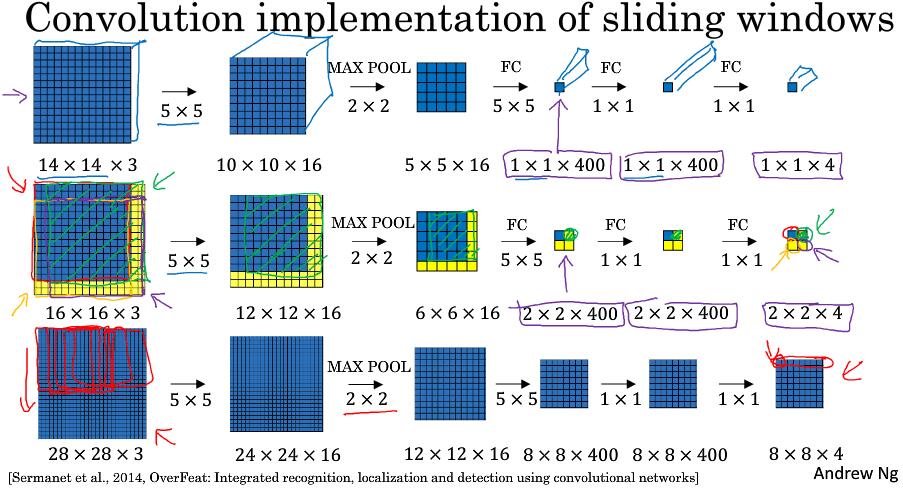
假如训练数据为14x14x3,而测试图片数据为16x16x3,按切分的话,可以将16x16x3切分成四部分,然后每部分输入网络进行计算。但这样需要计算四次,且重复计算区域较大。可以将16x16x3图片直接输入网络,得到的2x2x4分别代表切割的四部分结果。
3.5 Bounding Box预测 (Bounding box predictions)
参考论文:YOLO You Only Look Once: Unified real-time object detection 论文比较难懂。
上节讲到的滑动窗口卷积实现算法效率很高,但仍有一个问题,不能输出最精准的边界框。
YOLO(you only look once)算法:

假设输出维度为8:{px, bx, by, bh, bw, c1, c2, c3}。将原始100x100的图片划分为3x3的格子,对每个格子使用分配y标签(8维)。然后训练输出各个格子的y。最后整个输出为3x3x8的维度。
当然,你可以切分更细,使用19x19边框,这个单个边框内包含多个目标的可能性更小。
其中一个细节:bx,by,bw,bh都是[0,1]的,以每个边框的左上角为(0,0)坐标,右下角为(1,1)坐标。
3.6 交并集 (Intersection over union)
目标检测算法的评估参数:交并集(lou):$\frac{交集面积}{并集面积}$。一般lou>0.5。这个阈值可以人为设置,很少小于0.5。lou衡量了两个边界框的重叠相对大小。
3.7 非极大值抑制(Non-max suppression)
先假设对象检测中只有一种对象,但算法通常会检测出多次。如在19x19=361个格子检测,会得到很多格子检测包含目标,但很多检测的是同一个目标。
非极大值抑制是说,对于同一个检测物体的多个检测边界,仅输出最大概率的,抑制其它边界输出。
对于多目标类别检测,正确的做法是独立进行多次非极大值抑制。
3.8 Anchor Boxes
当两个识别目标居于同一个格子时候,该如何处理呢?之前的目标检测都只能在一个格子里检测一个对象。
以一个格子最多两个对象为例子,首先根据目标的特性人为规定两个Anchor Boxes,比如竖着的为人,横着的为车。然后格子的类别标签y不在是8维度,而是16维度。前8维度为Anchor Boxes1的标签,后八个维度为Anchor Boxes2的标签。
如何选择Anchor Boxes呢?可以使用K-Means对对象进行聚类,然后得到形状。
3.9 YOLO 算法
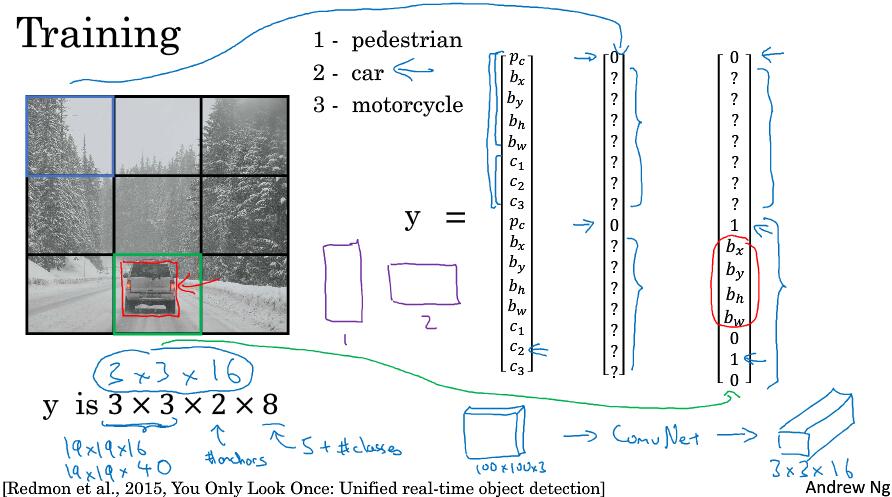
将训练集图片分成3x3格子,需要检测三类对象:行人,汽车,摩托车。使用两个anchor box。第一个格子和第八个格子的标签如图。
在预测的时候,一个目标的情况很容易理解。而对于下图: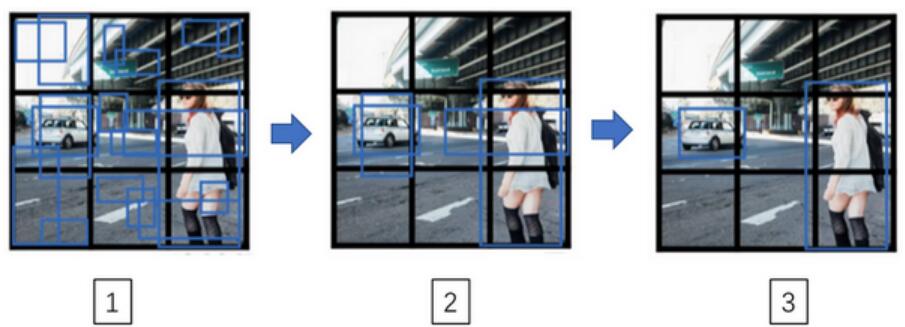
- 对于每一个grid call,得到两个预测边界框
- 去掉概率低的预测
- 对每个类别(行人,汽车,摩托车)使用非极值抑制算法。最后只得到最后一个预测。
3.10 R-CNN
首先得到候选区域,再进行CNN卷积识别。 - R-CNN 使用图像分割算法,选取候选区域,然后使用滑动窗口方式卷积
- Fast R-CNN 类似于第四节,不再单个框输入而是一次全部,但速度还是比较慢。
- Faster R-CNN 使用CNN来选择候选区域。
第4周
4.1 什么是人脸识别 (What is face recognition?)
人脸验证(Verification)
- 输入照片和姓名(ID)
- 输出图像是否为本人
人脸识别(Recognition)
- 拥有$K$个人脸的数据库
- 输入图像
- 输出人物ID如果他是$K$个人中之一
很显然,在人脸验证的任务中,准确率达到99%是可以接收的,但放到识别任务中,100个人则代表1%的失误状况,所以人脸识别需要较高的准确率。
人脸验证之所以困难,原因之一是要解决”一次学习(one-shot learning problem)“问题。
4.2 One-Shot学习 (One-Shot learning)
如果识别人有四个人,使用ont-hot来表示输出,这种方式不太好,如果新加入一个人脸,则ont-hot维度需要改变。同时,一半人物只有一张照片,使用一张照片不能有效训练完成一个稳健的神经网络。
为了解决One-Shot问题,可以使用”similarity“ function。使神经网络学习一个$d$表示的函数,$d(img1, img2) = degreed\ of \ difference\ between\ images$。它以两张图片作为输入,然受输出两张图片的差异值。差异值小于某个阈值$\tau$,它是一个超参数,表明是同一个人。
4.3 Siamese网络 (Siamese network)
论文:DeepFace closing the gap to human level performance
Siamese网络,学习函数$d$来计算两张人脸的相似度。
思想是,将人脸编码(映射)成固定维度向量(非one-hot)
将$x^{(1)}$和$x^{(2)}$的距离定义为这两幅图片的编码之差的范数,$d( x^{( 1)},x^{( 2)}) =|| f( x^{( 1)}) - f( x^{( 2)})||_{2}^{2}$。
如果$x^{(i)}$和$x^{(j)}$是同一个人,则$||f(x^{(i)}) - f(x^{(j)})||^2$很小,相反很大。使用反向传播来学习网络参数。如果定义真正的目标函数呢?使用三元组损失函数
4.4 Triplet损失 (Triplet loss)
论文:FaceNet: A Unified Embedding for Face Recognition and Clustering
Anchor Positive Negative
用三元组术语来说,对于一个Anchor图片,Positive图片和其是同一个人,距离更近,Negative非同一个人,距离更远。简写成$A$,$P$,$N$
三元组损失,我们的目标是想要$|| f(A) - f(P) ||^{2}$,你希望这个数值很小,准确地说,你想让它小于等$f(A)$和$f(N)$之间的距离,或者说是它们的范数的平方(即:$|| f(A) - f(P)||^{2} \leq ||f(A) - f(N)||^{2}$)。($|| f(A) - f(P) ||^{2}$)当然这就是$d(A,P)$,($|| f(A) - f(N) ||^{2}$)这是$d(A,N)$,你可以把$d$ 看作是距离(distance)函数,这也是为什么我们把它命名为$d$。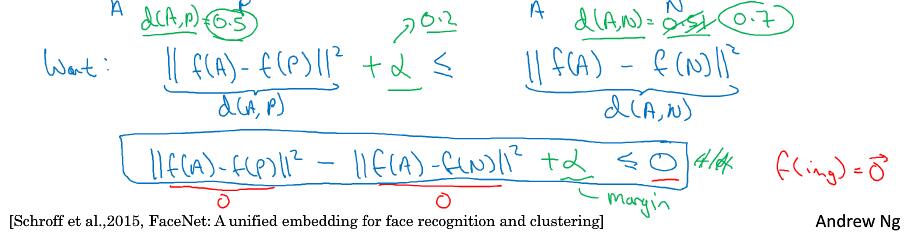
网络中的参数全为0的话,也是可以满足条件的,为了避免这个问题,添加一个超参数$\alpha$,代表间隔margin。
最后我们可以定义损失函数:
$$L(A,P,N) = max(||f(A) - f(P)||^2 - ||f(A) - f(N)||^2 + \alpha, 0)$$
不难发现,当$|| f( A) - f( P)||^{2} -|| f( A) - f( N)||^{2} + \alpha \ge 0$,则得到一个正的损失值。 相反,网络不会关心负值大小。
对于训练集,至少保证一个人有多张图片。训练的时候,可以随机选取照片来构成APN三元组,但使用相近图像的AP才能更好地训练网络。
人脸识别模型可以选择其它公司或研究机构训练好的网络模型。
4.5 面部验证与二分类 (Face verification and binary classification)
论文:DeepFace:Closing the gap to human-level performance in face verification
除了Triplet loss方法外,还可以把人脸识别看作二分类问题。
选取一堆Siamese网络,将两章图片进行编码(映射),然后输入逻辑回归单元如Sigmoid,进行输出1或0。此时损失函数为:
$$\hat{y} = \sigma ( \sum_{k=1}^{128} \omega_i |f(x^{(i)})_k - f(x^{(j)})_k| + b)$$
$f(x^{(i)})$是图片$x^{(i)}$的编码,$k$代表第$k$个元素。
这样就可以将其转化成二分类问题。
4.6 什么是神经风格转换 (What is neural style transfer)
我将使用$C$来表示内容图像,$S$表示风格图像,$G$表示生成的图像。
4.7 什么是深度卷积网络?(What are deep ConvNets learning?)
论文:Visualizing and Understanding Convolutional Networks
通过可视化卷积神经网络分析可以发现,层数越高,网络学习到的内容越复杂。
4.8 代价函数 (Cost function)
代价函数包含两部分:
- $J_{\text{content}}(C,G)$,内容代价函数,用来度量生成图片$G$的内容与内容图片$C$的内容有多相似。
- $J_{\text{style}}(S,G)$,风格代价函数,用来度量图片$G$的风格和图片$S$的风格的相似度。
最终的代价函数为($\alpha$ 是权重超参数):
$$J( G) = a J_{\text{content}}( C,G) + \beta J_{\text{style}}(S,G)$$
4.9 内容代价函数 (Content cost function)
$J( G) = \alpha J_{\text{content}}( C,G) + \beta J_{\text{style}}(S,G)$
内容代价函数:
- 选取隐层$l$来计算内容代价, use hidden layer l to compute content cost.
- 使用预训练的卷积神经网络,如VGG
- 使用$a^{[l]\lbrack C\rbrack}$和$a^{[l]\lbrack G\rbrack}$来表示两个图片$C$和$G$的$l$层的激活函数值。
- 如果这两个激活值相似,那么就意味着两个图片的内容相似。
内容代价函数求得就是两个图片之间$l$层激活值差值的平方和。
4.10 风格代价函数 (Style cost function)
论文:A neural algorithm of artistic style
风格的数据表达:相关性(correlation)
计算$l$层的输出,通道间的相关性。
风格矩阵(style matrix)
使用$a_{i,\ j,\ k}^{[l]}$来表示隐层$l$中$(i,j,k)$位置的激活项,$i$,$j$,$k$分别代表该位置的高度、宽度以及对应的通道数。计算风格矩阵$G^{l}$,它是一个$n_{c} \times n_{c}$的矩阵,同样地,我们也对生成的图像进行这个操作。
$G_{kk^{‘}}^{[l][S]} = \sum_{i = 1}^{n_{H}^{[l]}}{\sum_{j = 1}^{n_{W}^{[l]}}{a_{i,\ j,\ k}^{[l][S]}a_{i,\ j,\ k^{‘}}^{[l][S]}}}$
用符号$i$,$j$表示下界,对$i$,$j$,$k$位置的激活项$a_{i,\ j,\ k}^{[l]}$,乘以同样位置的激活项,也就是$i$,$ j$,$k’$位置的激活项,即$a_{i,j,k^{‘}}^{[l]}$,将它们两个相乘。然后$i$和$j$分别加到l层的高度和宽度,即$n_{H}^{[l]}$和$n_{W}^{[l]}$,将这些不同位置的激活项都加起来。$(i,j,k)$和$(i,j,k’)$中$x$坐标和$y$坐标分别对应高度和宽度,将$k$通道和$k’$通道上这些位置的激活项都进行相乘。我一直以来用的这个公式,严格来说,它是一种非标准的互相关函数,因为我们没有减去平均数,而是将它们直接相乘。
同样计算生成图像的的风格矩阵:
$G_{kk^{‘}}^{[l][G]} = \sum_{i = 1}^{n_{H}^{[l]}}{\sum_{j = 1}^{n_{W}^{[l]}}{a_{i,\ j,\ k}^{[l][G]}a_{i,\ j,\ k^{‘}}^{[l][G]}}}$
Gram matrix,所以用$G$来表示。
最后,整体的风格代价函数为两个风格矩阵的F范数的平方,可以乘以一个归一化常数,或者乘以一个超参数$\beta$就好了。
$J_{style}^{[l]}(S,G) = \frac{1}{(2n_H^{[l]}n_W^{[l]}n_C^{[l]})^2} \sum_k \sum_{k’}(G_{KK’}^{[l][S]} - G_{KK’}^{[l][G]})$
最终,整体的代价函数为:
$J(G) = a J_{\text{content}( C,G)} + \beta J_(S,G)$
4.11 一维到三维推广 (1D and 3D generalizations of models)
卷积操作可以应用到1D和3D上,1D可以使用序列模型,会在下次课程中讲解并对比。
应用到3D,channel层是额外的。