02.改善深层神经网络
第一周 深度学习的实用层面
1-1 训练/开发/测试集
以前一般使用7:3划分训练集测试集或6:2:2 。大数据下通常需要用验证集快速验证多种算法的优劣,所以可以去小一些。
百万数据集98:1:1%
确保验证集合测试集的数据来自同一分布
1-2 偏差/方差
欠拟合:偏差过高 过拟合:方差过高
高方差:训练集和验证集的错误率相差过大
高偏差:与人类等实际分类效果对比太差
如果可以确定最优方差 然后去和偏差方差作比较来评价模型
1-3 机器学习基础
High bias?
- Bigger network
- Train longer
- NN architecture search (可选)
拟合训练集后,再看 High variance? - More data
- regularization
- NN architecture search (可选)
1-4 正则化
L1 正则化 $\omega$稀疏,但没有压缩模型减少内存
L2 正则化又称权重衰减(Weight Decay) 公式可见权重在减小
1-5 为什么正则化可以减少过拟合
L2 正则化防止过拟合 直观经验是权重越多接近于0 模型越简单(存疑)
以Sigmoid为例 当权重过小时候,Sigmoid是接近线性的,整个网络是线性的从而使模型变为简单来减少过拟合
1-6 Dropout(Inverted dropout)
d3 = np.random.rand(a3.shape[0], a3.shape[1]) < keep_proba3 /= keep_prob
以Hinton论文中提出的Dropout在测试集上是将概率$p$应用到神经元的输出边上
为了简化测试集的操作,在训练时候每个神经元的输出都降低为权重$1/p$ 这样就不需要在测试集做额外操作
BN与Dropout的冲突
解决方式:1. 先使用BN后使用Dropout, 更甚仅在softmax前一层使用 2.使用Uout
1-7 理解Dropout
Dropout 有效性体现:
- 等效正则化,使网络更简单
- 神经元不在完全依赖特定的输入神经元
可以设置不同层$\omega$的dropout rate 设置为1表示不使用dropout
Dropout主要同于计算机视觉(CV),当过拟合的时候可以在使用
缺点:
- 损失函数的定义不对明确
- 调试困难(先固定为1, J递减再开启)
1-8 其他正则化技术
- Data Augmentation 数据增强 如 图片旋转、裁剪、扭曲
- early stooping have a mid-size rate $||W||_{2F}$
通常的训练步骤:- 优化代价函数J(GD/ Momentum/ RMRprop /Adam)
- 避免过拟合(正则化) | 减少方差(正交化)
early stooping 不能独立处理问题1 2
1-9 正则化输入 Normalization training sets
0均值 1方差
当特征范围不一致时候使用归一化,加速$J$下降
1-10 梯度消失和爆炸
1-11 神经网络的权重初始化
$z = W_1x_1+W_2x_2+…+W_nx_n$
设置$var(Wi) = 1/n W^{[l]} $=np.random.rand(shape)*np.sqrt(1/n[l-1])
最后一项
tanh 使用Xavier 初始化,ReLU使用公式2
Xavier 初始化,公式: $\sqrt{\frac{1}{n^{[l-1]}}}$
公式: $\sqrt{\frac{2}{n^{[l-1]}+n^{[i]}}}$
此超参数的调节优先等级比较低
1-12 梯度的数值逼近
双边误差法:$f(\theta) = \frac{f(\theta+\epsilon) - f(\theta-\epsilon)}{2\epsilon}$
1-13 梯度检验
$J(\theta) -> d\theta$
$10^{-7}$ 效果great $10^-3$效果wrong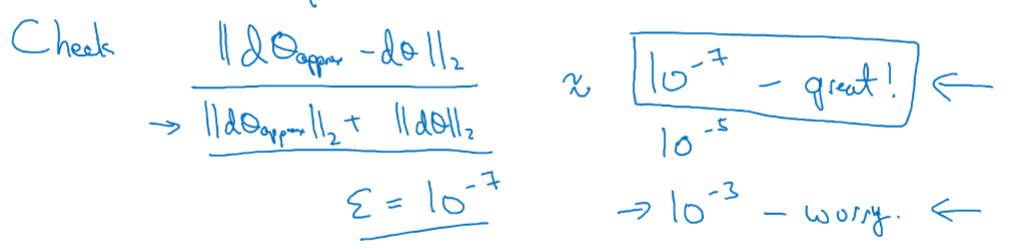
1-14 梯度检验经验
- Dont use in training - only to debug
- If algorithm fails grad check, look at components to try to identify bug
- Rember regularization
- Doesn’t work with dropout
- Run ai random initialization;perhaps again after some training
第一周第一次作业
权重初始化作用:
- 加速梯度收敛
- 增加泛化能力
权重初始化对比
- 0
- 随机
- HE三种方式
结果逐渐变好 其中He Initialization (Xavier Initialization变种 参考)
权重为0 $cost$不下降模型无效
权重过大,没有效果
第一周第二次作业
正则化技术很有效
第一周第三次作业
梯度检验:
$$difference = \frac {| grad - gradapprox |_2}{| grad |_2 + | gradapprox |_2 } \tag{3}$$
第二周 优化算法
2.1 Mini-batch梯度下降法
默认梯度下降是将所有数据进行计算实现一部梯度下降
分批次 : $X = {X^{\{1\}}, X^{\{1\}}, …, X^{\{m\}} }$
同样:$Y = \{Y^{\{1\}}, Y^{\{1\}}, …, Y^{\{m\}} \}$
mini batch $t:X^{\{t\}}, Y^{\{t\}}$
$x^{(i)}$表示训练集中第$i$个训练样本
$z^{[l]}$表示神经网络的层数
$X^{\{i\}} \ Y^{\{i\}}$表示不同的mini batch $X$维度$(n_x, \text{batch size})$
1 | # 遍历批次 每批次使用向量化 |
2.2 理解mini-batch梯度下降法
损失表现
mini-batch 的成本函数是震荡下降的
选择mini-batch size
Tips:
- 将mini-batch size 设置为m : Batch Gradient Descend
- 将mini-batch size 设置为1 : stochastic gradient descent(随机梯度下降)
batch gradient descend的cost轨迹,相对噪声低,幅度大
stochastic gradient descent的cost轨迹,噪声大,徘徊在最小值 缺点:失去了向量化的加速处理
一般使用合适batch size的mini-batch 其优点:
- 向量化
- 不全部使用数据集
size 选取:
- 样本集小直接使用batch gradient descent ($m\leqslant 2000$)
- mini-batch size 一般为 [64,128,256,512] 一般为2的次方
- 保证$X^{\{t\}}, Y^{\{t\}}$ 与CPU/GPU内存相适应
2.3 指数加权平均
指数加权平均(exponentially weighted averages)又称指数加权移动平均(exponentially weight moving averages)
以温度为例,
$V_0 = 0 \\
V_1 = 0.9 \cdot V_0 + 0.1 \cdot \theta_1 \\
V_2 = 0.9 \cdot V_1 + 0.1 \cdot \theta_2 \\
V_3 = 0.9 \cdot V_2 + 0.1 \cdot \theta_3 \\
… \\
V_t = 0.9 \cdot V_{t-1} + 0.1 \cdot \theta_t$
效果如图: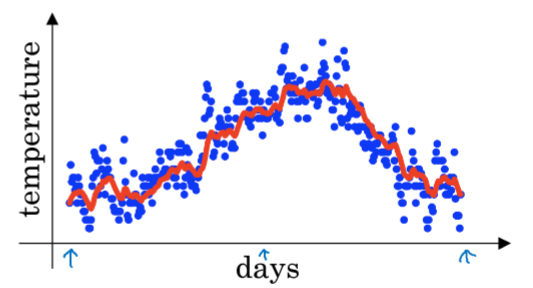
$V_t = \beta V_{t-1} + (1-\beta) \theta_t$
当 $\beta = 0.9 :\approx \frac{1}{1-\beta} = 10\ (dayTemperature)$
当 $\beta = 0.98 :\approx \frac{1}{1-\beta} = 50\ (dayTemperature)$
当 $\beta = 0.5 :\approx \frac{1}{1-\beta} = 2\ (dayTemperature)$
对比效果图如下: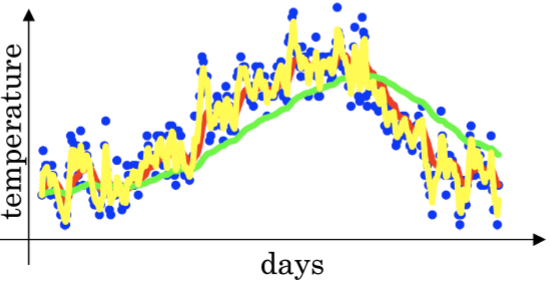
红色0.9(10天平均温度) 绿色0.98(50天平均温度) 黄色0.5(2天平均温度)
平均天数越大图像越平滑,越偏移
平均天数越小噪声越大
选定参数对模型有一定的影响
2.4 理解指数加权平均
$v_t = \beta v_{t-1}+(1-\beta)\theta_t$
$V_{100} = 0.9v_{99}+0.1\theta_{100} \\
V_{99} = 0.9v_{98}+0.1\theta_{99} \\
V_{98} = 0.9v_{97}+0.1\theta_{98} \\
… \\
V_{100}=0.1\cdot\theta_{100}+0.1\cdot0.9\theta_{99}+0.1\cdot(0.9)^2\theta_{98}+0.1\cdot (0.9)^3\theta_{97}…$
$$0.9^{10} \approx 0.35 \approx \frac{1}{e} \label{1}$$
$$(1-\epsilon)^{\frac{1}{\epsilon}} \approx \frac{1}{e}$$
即,经过10天后,权重下降到原来的三分之一
当$\beta = 0.98$时,需要指数50能达到$\frac{1}{\epsilon}$,即可以看作是平均了50天温度可以使用$$\frac{1}{1-\beta}$$来表示平均了多少数据(非正式数学证明)
2.5 指数加权平均的偏差修正(bias correction)
当$t_0 = 0$时,$V_1 = \beta V_0+(1-\beta )\theta_1 = (1-\beta )\theta_1$,会发现前期数据值比较小 。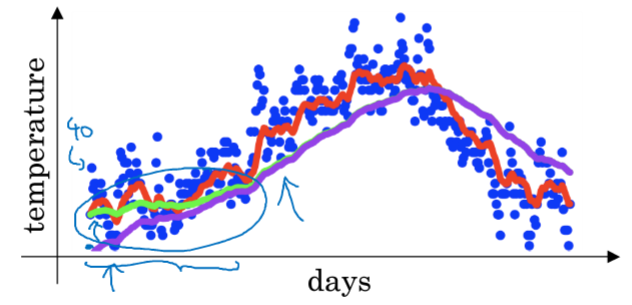
紫线是实际图形,对比绿线发现,前期数值偏小,后期重合
偏差修正$\frac{V_t}{1-\beta^t}$ 用来解决前期偏差过大问题,随着$t$的增加,偏差修正无效。
在机器学习中,大家都不在乎使用偏差修正,大部分人喜欢熬过前期。如果关心初期的偏差,就需要使用它。
2.6 动量梯度下降法Momentum
Momemtum 在梯度下降中,我们希望朝最优解进向横向速度越大,纵向震荡越小越好。
Momemtum对于优化碗形状损失函数比较适用
Implementation details
On iteration t:
compute $dW$,$db$, on the current mini-batch
$v_{dW} = \beta v_{dW}+(1-\beta)dW \\
v_{db} = \beta v_{dWb}+(1-\beta)db \\
W = W -\alpha v_{dW}, b=b-\alpha v_{db}$
Hyperparameters:$\alpha ,\beta$ $\beta = 0.9$(平均十次数据) 不使用偏差修正
$dW$ $db$ 可以理解为加速度
$v_{dW}, v_{db}$ 可以理解为速度
前项$\beta < 1$可以理解为摩擦力
Tip: 有一些资料中删除了后项的$(1-\beta)$参数, 即$v_{dW} = \beta v_{dW}+dW$
得到的$v_{dW}$缩小了$(1-\beta)$倍
这要求学习率$\alpha$要与$(1-\beta)$相应变化,影响了$\alpha$的最优值
此外,如果调整$\beta$ 则需要对应调整$\alpha$ 所以不选择此实现方式
2.7 RMSprop
RMSprop(root mean square prop)可以消除梯度下降算法中的摆动,加速梯度下降,可以使用更大学习率
我们希望在 $\text{w_}$ 更新更快,在 $\text{b_}$ 减小震荡
从一个蓝色箭头中可以看出$dw$比较大,$db$比较小(即梯度)
因此在更新时候加上相关项来处理
$\text{w_}$ 和 $\text{b_}b$ 表示高维中的参数 不仅代表w,b
实现:
在迭代$t$中
计算 mini-batch 中的$dw$,$db$
$S_{dw} = \beta S_{dw} + (1-\beta)(dw)^2$
$S_{db} = \beta S_{db} +(1-\beta)(db)^2$
$w = w-\alpha \frac{dw}{\sqrt{S_{dw}}}$
$b = b- \alpha \frac{db}{\sqrt{S_{db}}}$
$(dw)^2$ 变小 w更新越大 $(db)^2$ 变大 b更新越大
特别的为了防止 $\sqrt{S_{dw}}$ 过小,会添加一项 $\epsilon$ : $w = w-\alpha \frac{dw}{\sqrt{S_{dw}+\epsilon}}$ $b = b- \alpha \frac{db}{\sqrt{S_{db}+\epsilon}}$ $\epsilon$ 一般取值 $10^{-8}$
效果示意图为绿线
2.8 Adam 优化算法
Adam优化算法是把Momentum和RMSprop算法结合在一起
算法流程:
$V_{dw} = 0, S_{dw} = 0, V_{db} = 0, S_{db} = 0$
在迭代$t$:
使用mini-batch 计算 $dw$, $db$
$V_{dw} = \beta_1V_{dw}+(1-\beta_1)dw, V_{db} = \beta_1v_{db}+(1-\beta_1)db $ <- “momentum” $\beta_1$
$S_{dw} = \beta_2S_{dw}+(1-\beta_2)(dw)^2, S_{db} = \beta_2S_{db}+(1-\beta_2)(db)^2 $ <- “RMSprop” $\beta_2$
# 要进行偏差修正
$V_{dw}^{corrected} = V_{dw}/(1-\beta_1^t), V_{db}^{corrected} = V_{db}/(1-\beta_1^t)$
$S_{dw}^{corrected} = S_{dw}/(1-\beta_2^t), S_{db}^{corrected} = S_{db}/(1-\beta_2^t)$
# 更新系数
$W=W-\alpha \cdot \frac{V_{dw}^{corrected}}{\sqrt{S_{dw}^{corrected}+\epsilon}}, b = b-\alpha\cdot\frac{V_{db}^{corrected}}{\sqrt{S_{dw}^{corrected}+\epsilon}}$
超参数的选择
$\alpha : 需要调整$
$\beta_1:0.9 ->(dw)$
$\beta_2:0.999 ->(dw^2)$
$\epsilon:10^{-8}$
一般使用默认就好,不需要特别修改
Adam : Adaption momentum Estimator
2.9 学习率衰减
epoch:完整的使用一次全部数据集
- $\alpha = \frac{1}{1+decay_rate*epoch_num}$
- $\alpha = 0.95^{epoch_num}\cdot \alpha_0$
- $\alpha = \frac{k}{\sqrt{epoch_num}}\cdot \alpha_0$
- 离散化衰减
- 手动衰减
2.10 局部最优的问题
鞍点(saddle point)问题:在各维度导数为0,但部分维度是凸函数顶点
- unlikely to get stuck in a bad local optima(不太可能陷入局部最优的最佳点)
- Plateaus can make learning slow(平滑区域导致学习变慢,Adam能加速学习逃离)
第二周作业
Momentum
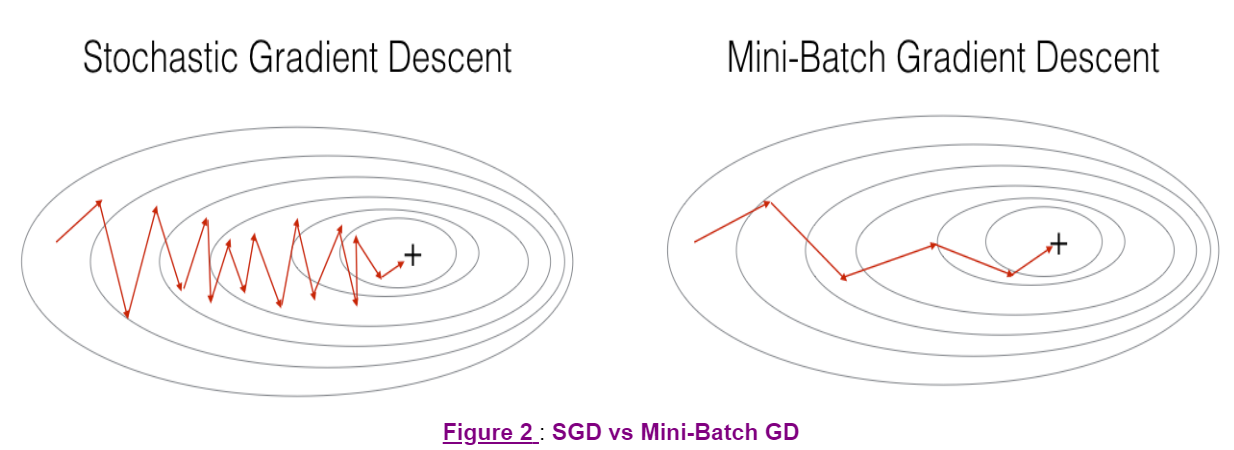
- 随机梯度下降和批量梯度下降的区别在于,在一次计算梯度时候所使用的训练集样本数量(The difference between gradient descent, mini-batch gradient descent and stochastic gradient descent is the number of examples you use to perform one update step.)
- 必须调整学习率(You have to tune a learning rate hyperparameter $\alpha$ .)
- 参数设置很好的批量梯度下降算法,比梯度下降和随机梯度下降算法要高效,特别在数据集大情况下(With a well-turned mini-batch size, usually it outperforms either gradient descent or stochastic gradient descent (particularly when the training set is large).)
Adam
$$
\begin{cases}
v_{W^{[l]}} = \beta_1 v_{W^{[l]}} + (1 - \beta_1) \frac{\partial J }{ \partial W^{[l]} } \\
v_{W^{[l]}}^{corrected} = \frac{v_{W^{[l]}}}{1 - (\beta_1)^t} \\
s_{W^{[l]}} = \beta_2 s_{W^{[l]}} + (1 - \beta_2) (\frac{\partial J }{\partial W^{[l]} })^2 \\
s_{W^{[l]}}^{corrected} = \frac{s_{W^{[l]}}}{1 - (\beta_2)^t} \\
W^{[l]} = W^{[l]} - \alpha \frac{v_{W^{[l]}}^{corrected}}{\sqrt{s^{corrected}_{W^{[l]}}}+\varepsilon}
\end{cases}
$$
- 适合mini-batch 和 momentum
- 稍微调整超参数就能很有效($\alpha$除外)
第三周 超参数调试、Batch正则化和程序框架
3.1 调试处理
系统超参数调试技巧
$\alpha$ 第一级别重要
$\beta$(默认0.9) mini-batch size 和 #hidden units 第二级别重要
learning rate decay 和 #layers 第三级别重要
$\beta_1(0.9),\beta_2(0.999), \epsilon(10^{-8})$基本不用修改
超参数搜索原则:先随机取值再精确搜索
随机取值:不是网格取值
精确搜索:缩小范围
3.2 为超参数选择合适的范围
对参数选择良好的尺度(scale),不是使用区间随机取值,而是将区间通过指数变换成整数值来随机抽取。
如学习率$\alpha$范围为[0.0001, 1],直接随机抽取,搜索资源90%会落在[0.1,1]1
2r = -4 * np.random.rand() #[-4, 0]
alpha = 10 ** r #[10^-4, 10^0]
3.3 超参数选取实战:Pandas vs. Caviar
- Pandas:在CPU/GPU资源较少的情况下,在一个模型上不同时间调整学习率,查看损失函数表现
- Caviar:在计算资源充足条件下,并行跑多个模型,选择最好的模型参数
3.4 正则化网络的激活函数 Batch Normalization
吴恩达推荐的是在激活函数之前对$Z$进行归一化,与BN网络论文一致。参考论文:BN_PDFD和BN笔记
BN与Dropout的冲突
解决方式:1. 先使用BN后使用Dropout, 更甚仅在softmax前一层使用 2.使用Uout
$$
\mu = \frac{1}{m}\sum_i z^{(i)}
$$
$$
\sigma^2 = \frac{1}{m}\sum_i(z^{(i)}-\mu)^2
$$
$$
z_{norm}^2=\frac{z^{(i)}-\mu}{\sqrt{\sigma^2+\epsilon}}
$$
$$
\bar{z}^{(i)} = \gamma z_{norm}^{(i)} + \beta
$$
$\gamma$和$\beta$是为了防止归一化限制输入特征的的表现。
当$\gamma = \sqrt{\sigma^2+\epsilon}$,$\beta=\mu$,只是一个恒等函数。
3.5 将Batch Normalization 拟合进神经网络
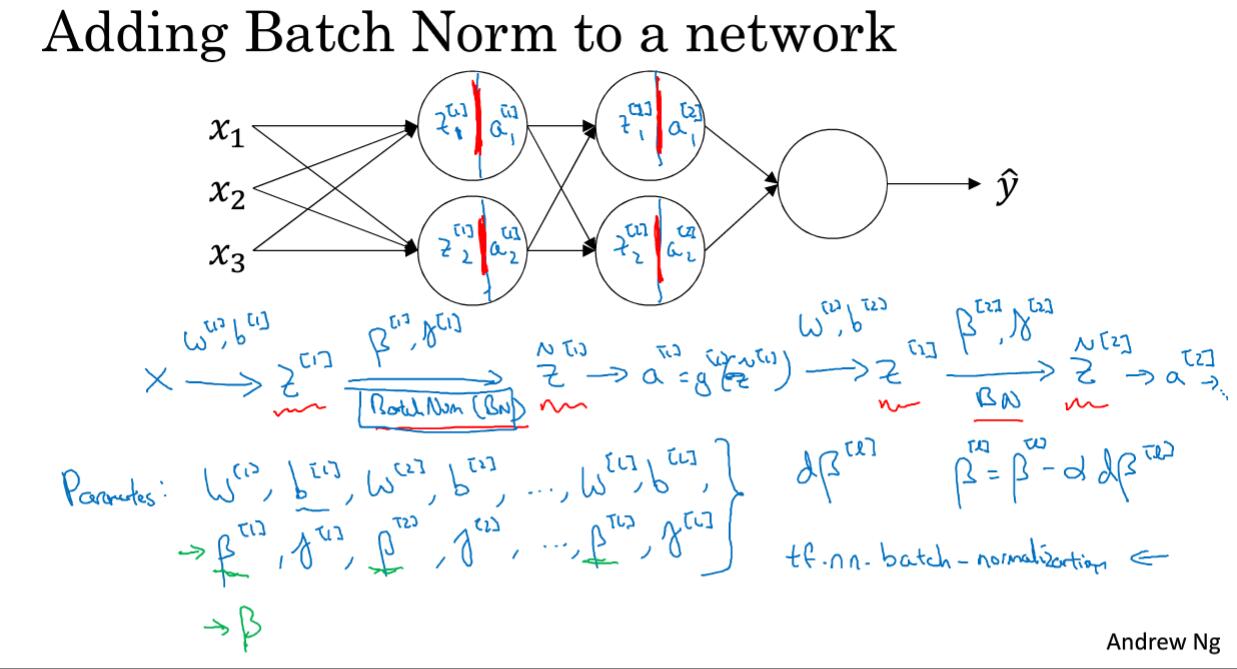
BN应用在每一个神经元激活函数之前的计算结果$z$,同时BN使参数偏置项$b$无效
[Appendix] 神经网络训练步骤
BN与Dropout的冲突
解决方式:1. 先使用BN后使用Dropout, 更甚仅在softmax前一层使用 2.使用Uout
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
set hyper parameters:
batch_size
learning_rate learning_rate_decay
beta1,beta2
keep_probe
init parameters(He Initialization):
w,
gamma,beta #?存疑
for e in epoch:
for i in iteration:
# 1. forward propagation
# 1.1 compute Z (dw)(db deprecated by BN)
Z = W * a
# 1.2 BN (dgamma,dbeta)
Z = BN(Z)
# 1.3 activation function
a = g(Z)
# ... iterate L neural layer
# gradient parameters: dw,dgamma,dbeta
# 1.4 droupout (applied on last hidden layer)
a = a * d
a /= keep_prob
# 2. back paopagation
dw, db, dbeta = computeGradient(Z)
# 2.1 momentum
vdw = beta1 * vdw + (1-beta1) * dw
vdw_corrected = vdw/(1-beta1 ** i)
# same as other gradient parameters
# 2.2 RMSprop
sdw = beta2 * sdw + (1-beta2) * dw ** 2
sdw_corrected = sdw/(1-beta2 ** i)
# 2.3 update parameters
w = w - learning_rate * ( vdw_corrected / math.sqrt(sdw_corrected + episilon) )
# same as other gradient parameters
3.6 Batch Norm 为什么奏效
- 归一化使输入均值为0,方差为1,能够加速学习。
- 固定了各神经层间的输入分布变化,因而使神经元能更好地学习
BN的额外功能:正则化
- 数据被缩放
- 添加噪声,使神经元不再特定依赖
- 轻微的正则化效果
3.7 测试时的 Batch Norm
和BN论文说明不太相同。
在训练BN网络地时候,
训练数据集分为$X ^{\{1\}}$,$X^{\{2\}}$,$X^{\{3\}}$…$X^{\{m\}}$
对于第一层地一个神经元可以得到$X^{\{1\}[1]}$,$X^{\{2\}[1]}$,$X^{\{3\}[1]}$……
每一层的每一个神经元,都会得到$m$个$\mu$和$\sigma$
以第l层第n个神经元为例,将其$m$个$\mu$使用指数加权平均方法进行处理
$v_i = \beta v_{i-1} + (1-\beta)\mu^{\{i\}}$
在测试集的时候
BN仅仅是一个线性变化,
利用指数加权平均计算各层神经元的$\mu$和$\sigma$参数
3.8 Softmax 回归
$$
y(a^{[L]})= \frac{e^{z^{[L]}}}{\sum z^{[L]}}
$$
Softmax 用来归一化概率
Softmax 激活函数的特殊:输入为向量,输出为向量,其它激活函数输入为单值
无隐层的Softmax网络可以用于多分类,学习到的决策边界都是线性的。
3.9 训练一个Softmax分类器
softmax是和hardmax相对应的。(hardmax形式[0,1,0,0])
Softmax regression generalizes logistic regression to C classes
Softmax是logistic的多分类应用。
Loss Function:
$$L(\hat{y},y)=-\sum_{j=1}^C y_j log\hat{y}_j$$
如$C=4$,$y=[0,1,0,0]$,$a^{[L]}=\hat{y}=[0.3,0.2,0.1,0.4]$,则:
$$L(\hat{y},y)=0+y_2 \dot log\hat{y}_2+0+0=-log\hat{y}_2$$
即损失函数定义是正确类别的概率越大(最大似然估计)
训练集的代价函数$$J=(\omega^{[i]},b^{[i]}…)=\frac{1}{m}\sum_{i=1}^m L(\hat{y},y)$$
实现梯度下降:$$\frac{\partial J}{\partial z^{[L]}} = dz^{[L]} = \hat{y}-y$$
深度学习框架
选择指标:
- 易于编程
- 运行速度
- 真正开源
部分深度学习框架:
- Caffe/Caffe2
- PyTorch
- Keras
- Tensorflow
- Theano
- mxnet