特征工程是什么？

有这么一句话在业界广泛流传：数据和特征决定了机器学习的上限，而模型和算法只是逼近这个上限而已。那特征工程到底是什么呢？顾名思义，其本质是一项工程活动，目的是最大限度地从原始数据中提取特征以供算法和模型使用。通过总结和归纳，人们认为特征工程包括以下方面：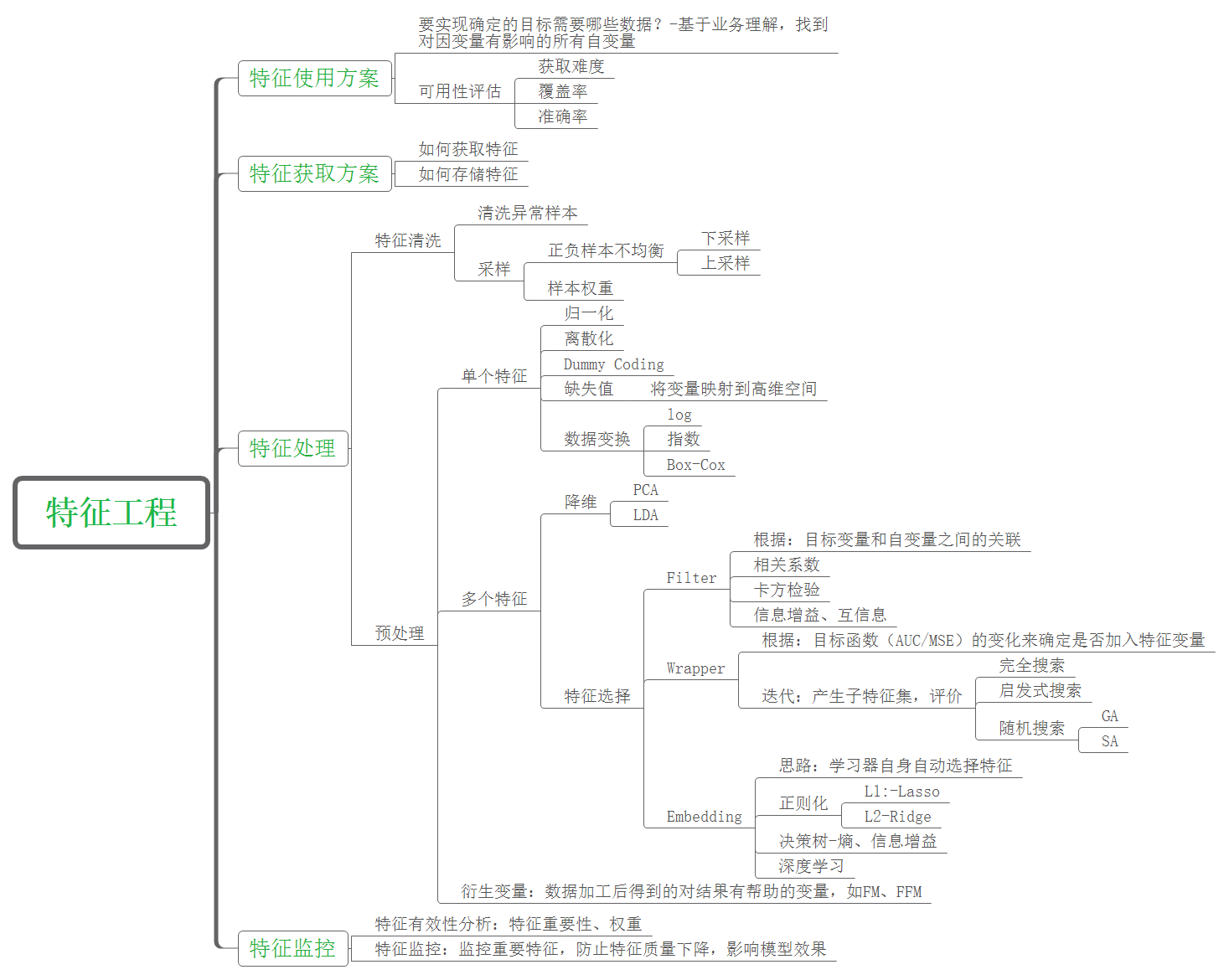

数据预处理

未处理的特征可能有以下问题：

不属于同一量纲：即特征的规格不一样，不能够放在一起比较。无量纲化可以解决这一问题。
信息冗余
定性特征不能直接使用
存在缺失值
信息利用率低

无量纲化

无量纲化能使不同规格(范围)的数据转换到同一规格(范围)。常用的无量纲化方法包括标准化和区间缩放法。标准化的前提使特征值服从正态分布，标准化后，其转化成正态分布。区间缩放法利用了边界值信息，将特征的取值区间缩放到某个特征的范围，例如[0,1]。

常用的方法及划分，网络上的资料负责多样。维基百科中Feature scaling(特征缩放)包含四种方式：Rescaling (min-max normalization)、Mean normalization、Standardization、Scaling to unit length。

Standardization

翻译问题：Normalization可以翻译成标准化或归一化，但是根据不同的用途(公式)其理解不同。

通常使用方法：Z-Score标准化
$$x^\prime = \frac{x-\mu}{\sigma}$$
这会将特征数据转换成均值为0，方差为1。其方法可以使用sklearn.preprocessing.StandardScaler

Normalization

Min-Max Normalization
$$x^\prime = \frac{x-mean(x)}{max(x)-min(x)}$$
这将特征数据缩放到[0,1]范围，可以使用sklearn.preprocessing。 MinMaxScaler

对定量特征二值化

设置阈值，大于阈值用1表示，相反用0表示。

对定性特征哑编码(one-hot)

对类别特征可以使用One-hot编码。

处理缺失值

特征选择

当数据预处理完成后，我们需要选择有意义的特征输入机器学习的算法和模型进行训练。通常来说，从两个方面考虑来选择特征：

特征是否发散：如果一个特征不发散，例如方差接近于0，也就是说样本在这个特征上基本上没有差异，这个特征对于样本的区分并没有什么用。
特征与目标的相关性：这点比较显见，与目标相关性高的特征，应当优选选择。除方差法外，本文介绍的其他方法均从相关性考虑。

根据特征选择的形式又可以将特征选择方法分为3种：

Filter：过滤法，按照发散性或者相关性对各个特征进行评分，设定阈值或者待选择阈值的个数，选择特征。
Wrapper：包装法，根据目标函数（通常是预测效果评分），每次选择若干特征，或者排除若干特征。
Embedded：集成法，先使用某些机器学习的算法和模型进行训练，得到各个特征的权值系数，根据系数从大到小选择特征。类似于Filter方法，但是是通过训练来确定特征的优劣。

Filter

方差选择法

使用方差选择法，先要计算各个特征的方差，然后根据阈值，选择方法大于阈值的特征。

卡方检验

经典的卡方检验是检验定性自变量对定性因变量的相关性。其根本思想就是在于比较理论频数和实际频数的吻合程度或拟合优度问题。假设自变量有N种取值，因变量有M种取值，考虑自变量等于i且因变量等于j的样本频数的观察值与期望的差距，构建统计量：

$$x^2 = \sum \frac{(A-E)^2}{E} = \sum_{i=1}^k \frac{(A_i - E_i)^2}{E_i} = \sum_{i=1}^{k} \frac{(A_i - np_i)}{np_i}$$

其中，Ai为i水平的观察频数，Ei为i水平的期望频数，n为总频数，pi为i水平的期望频率。

可以使用sklearn.feature_selection.chi2

互信息法

经典的互信息也是评价定性自变量对定性因变量的相关性的：

$$I(X;Y)=\sum_{x\in X} \sum_{y\in Y} p(x,y)\log \frac{p(x,y)}{p(x)p(y)}$$

在机器学习领域，互信息与信息增益是等价的。待重新确认。

Wrapper

递归特征消除法

递归消除特征法使用一个基模型来进行多轮训练，每轮训练后，消除若干权值系数的特征，再基于新的特征集进行下一轮训练。使用feature_selection库的RFE类来选择特征。

Embedded

基于惩罚项的特征选择法(L1,L2)

L1,L2以及Droup等归于深度学习中的正则化技术进行总结。

信息增益